2010-I-12

$\begin{array}{cl}
= & \dfrac{24-18}{6-(-2)} \\
= & \dfrac{3}{4}
\end{array}$

所以，通過 $A$ 和 $B$ 的直線的方程為

$\begin{array}{rcl}
y-24 & = & \dfrac{3}{4}(x-6) \\
4y-96 & = & 3x-18 \\
3x-4y+78 & = & 0
\end{array}$

$\begin{array}{rcl}
m_{AB}\times m_{AC} & = & -1 \\
\dfrac{3}{4}\times \dfrac{24-0}{6-x} & = & -1 \\
72 & = & -4(6-x) \\
4x & = & 96 \\
x & = & 24
\end{array}$

所以，點 $C$ 的坐標為 $(24,0)$。

$\begin{array}{cl}
= & \dfrac{1}{2} \left| \begin{array}{cc} 6 & 24 \\ -2 & 18 \\ 24 & 0 \\ 6 & 24 \end{array} \right| \\
= & \dfrac{1}{2} ( 6\times 18 + (-2)\times 0 + 24 \times 24 -24\times (-2) -18\times 24 – 0 \times 6) \\
= & 150 \text{ 平方單位}
\end{array}$

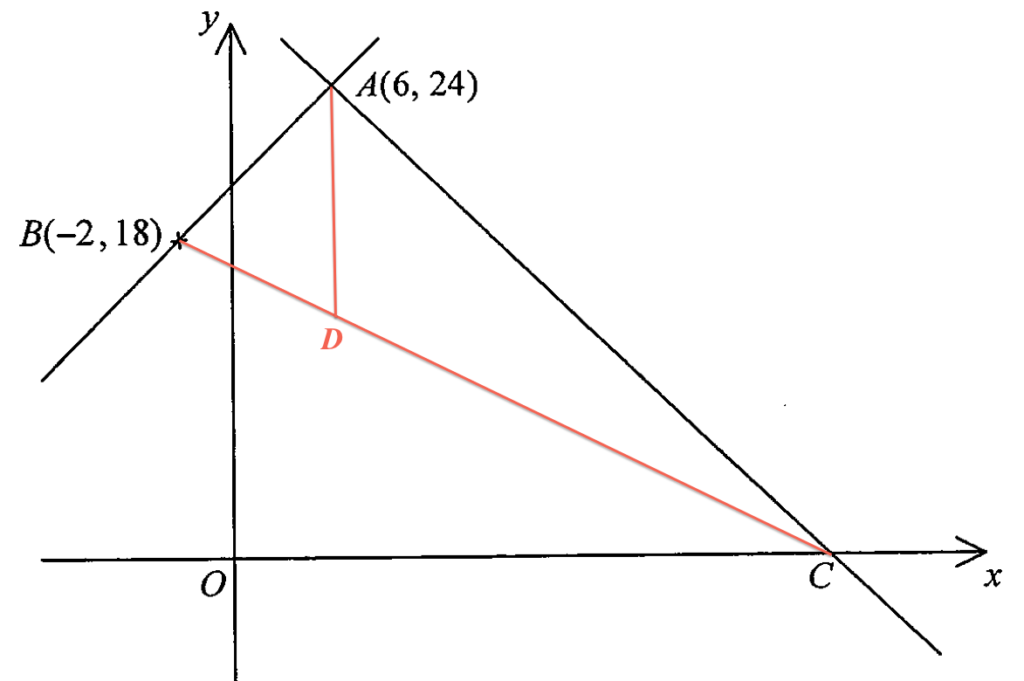
根據上圖，我們可以見到 $\Delta ABD$ 及 $\Delta ACD$ 的高相等。由此，可得

$\begin{array}{cl}
& BD:DC \\
= &\Delta ABD \text{ 的面積}: \Delta ADC\text{ 的面積} \\
= & 90 : 150-90 \\
= & 3 : 2 \\
= & \dfrac{3}{2} : 1
\end{array}$

所以，$r$ 的值為 $\dfrac{3}{2}$。