答案:A
標示 $O$ 為該半圓的圓心,並連結 $OD$。留意該半圓的半徑為 $13\text{ cm}$。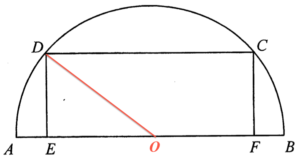
標示 $O$ 為該半圓的圓心,並連結 $OD$。留意該半圓的半徑為 $13\text{ cm}$。

$\begin{array}{rcl}
OE & = & OA – AE \\
& = & 13 – 1 \\
& = & 12 \text{ cm}
\end{array}$
因為 $CDEF$ 為一長方形,$\angle DEO = 90^\circ$。則利用畢氏定理,可得
$\begin{array}{rcl}
DE & = & \sqrt{OD^2 – OE^2} \\
& = & \sqrt{13^2 – 12^2} \\
& = & 5 \text{ cm}
\end{array}$
所以,長方形 $CDEF$ 的面積
$\begin{array}{cl}
= & DE \times EF \\
= & 5 \times 2 \times OE \\
= & 5 \times 2 \times 12 \\
= & 120 \text{ cm}^2
\end{array}$

