答案:B
標示 $O$ 為圓 $ABCD$ 的圓心,及 $Z$ 為 $BC$ 的中點。由此,$OZ \perp BC$。參考下面的圖像。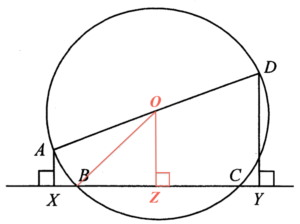
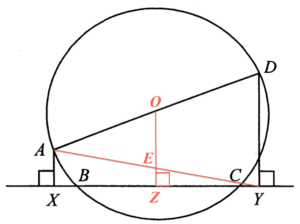
標示 $O$ 為圓 $ABCD$ 的圓心,及 $Z$ 為 $BC$ 的中點。由此,$OZ \perp BC$。參考下面的圖像。

留意 $OB=OA= 10\text{ cm}$ 及 $BZ = ZC = 6 \text{ cm}$。利用畢氏定理於 $\Delta OBZ$,可得
$\begin{array}{rcl}
OZ^2 & = & OB^2 – BZ^2 \\
OZ & = & \sqrt{10^2 – 6^2} \\
& = & 8\text{ cm}
\end{array}$
由於 $AO=OD$ 及 $AX//OZ//DY$,則根據截線定理,可得 $XZ = ZY$。

連結 $AY$,並標示 $E$ 為 $AY$ 及 $OZ$ 的交點。考慮 $\Delta ADY$。由於 $AO=OD$ 及 $OE//DY$,則根據截線定理,可得 $AE = EY$。因為 $AO=OD$ 及 $AE = EY$,則根據中點定理,可得 $DY = 2OE$。
考慮 $\Delta AXY$。由於 $AE = EY$ 及 $XZ = ZY$,則根據中點定理,可得 $AX = 2 EZ$。由此,可得
$\begin{array}{rcl}
AX + DY & = & 2 EZ + 2 OE \\
& = & 2 (OE + EZ) \\
& = & 2 OZ \\
& = & 2 \times 8 \\
& = & 16 \text{ cm}
\end{array}$

