答案:D
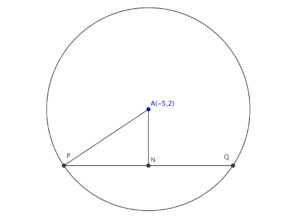

標示 $A$ 為所求的圓的圓心,及 $N$ 為 $PQ$ 的中點。所以,$\angle ANP = 90^\circ$。由於 $P$ 及 $Q$ 位於 $x$ 軸之上,$A$ 與 $PQ$ 的距離為 $2$。由此 $AN = 2$。利用畢氏定理於 $\Delta APN$,可得
$\begin{array}{rcl}
AP^2 & = & AN^2 + PN^2 \\
AP & = & \sqrt{2^2 + 3^2} \\
& = & \sqrt{13}
\end{array}$
所以,該圓的半徑為 $\sqrt{13}$。由此,該圓的方程為
$\begin{array}{rcl}
(x-(-5))^2 + (y-2)^2 & = & (\sqrt{13})^2 \\
x^2 + 10x +25 + y^2 -4y +4 – 13 & = & 0 \\
x ^ 2 +y^ 2 +10x – 4y +16 & = & 0
\end{array}$

