2011SP-I-19

1. 連結 $CD$。
   

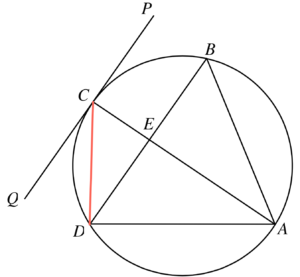
   $\angle QCD = \angle CDE$ (內角，$PQ//BD$)

   $\angle QCD = \angle DAE$ (內錯弓形上的圓周角)

   $\angle CDE= \angle BAE$ (同弓形上的圓周角)

   $\therefore \angle DAE = \angle BAE$。

   $AD=AB$ (已知)

   $AE=AE$ (公共邊)

   $\therefore \Delta ABD\cong \Delta ADE$ (S.A.S.)

2. $\because BE = DE$ ($\cong \Delta$的對應邊)$\therefore AE$ 為中線。

   $\therefore$ 形心在 $AE$ 之上。

   $\because \angle BAE = \angle DEA$ (已證)

   $\therefore AE$ 為 $\angle BAD$ 的角平分線。

   $\therefore$ 外心在 $AE$ 之上。

   \vspace{2mm}$\because \angle AEB = \angle AED$ ($\cong \Delta$的對應角)

   $\therefore AE \perp BD$

   $\therefore AE$ 為 $\Delta ABD$ 的垂高。

   $\therefore$ 垂心在 $AE$ 之上。

   $\because AE \perp BD$ 及 $BE=DE$，

   $\therefore AE$ 為 $BD$ 垂直平分線。

   $\therefore$ 內心在 $AE$ 之上。

   $\therefore \Delta ABD$ 的內心、垂心、形心與外心共線。

化簡之後，可得

$\left\{ \begin{array}{ll}
14D+4E+F=-212 & \ldots \unicode{x2460} \\
8D+12E+F=-208 & \ldots \unicode{x2461} \\
4D+4E+F = -32 & \ldots \unicode{x2462}
\end{array} \right.$

$\unicode{x2460} – \unicode{x2462}$，可得

$\begin{array}{rcl}
10D & = & -180 \\
D & = & -18
\end{array}$

$\unicode{x2461} – \unicode{x2462}$，可得

$\begin{array}{rcl}
4D+8E & = & -176 \\
E & = & -13 \\
\end{array}$

把 $D=-18$ 及 $E=-13$ 代入 $\unicode{x2462}$，可得

$\begin{array}{rlc}
4(-18)+4(-13)+F & = & -32 \\
F & = & 92 \\
\end{array}$

$\therefore$ 該圓的方程為 $x^2+y^2-18x-13y+92=0$。

由於 $PQ//BD$，它們的斜率相同。

$PQ$ 的斜率

$\begin{array}{cl}
= & BD \mbox{ 的斜率} \\
= & \dfrac{12-4}{8-4} \\
= & 2
\end{array}$

設 $y=2x+c$ 為 $PQ$ 的方程。

$\left\{ \begin{array}{ll}
x^2+y^2-18x-13y+92=0 & \ldots \unicode{x2463}\\
y=2x+c & \ldots \unicode{x2464}
\end{array} \right.$

把 $\unicode{x2464}$ 代入 $\unicode{x2463}$，可得

$\begin{array}{rcl}
x^2+(2x+c)^2-18x-13(2x+c)+92 & = & 0 \\
5x^2+(4c-44)x +(c^2-13c+92) & = & 0
\end{array}$

因為 $PQ$ 為圓的切線，所以

$\begin{array}{rcl}
\Delta & = & 0 \\
(4c-44)^2-4(5)(c^2-13c+92) & = & 0 \\
c^2+23c -24 & = & 0 \\
(c-1)(c+24) & = & 0
\end{array}$

$\therefore c=1$ 或 $c=-24$ (捨去)。

$\therefore PQ$ 的方程為 $y=2x+1$。