2012-II-21

答案：D
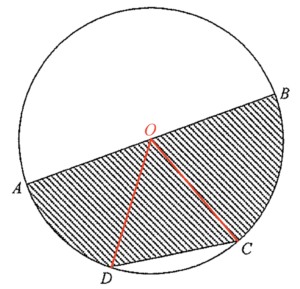
設 $O$ 為圓心。連結 $OD$ 及 $OC$。

留意 $OA$、$OB$、$OC$ 及 $OD$ 均為半徑，且半徑為 $6 \mbox{ cm}$。所以 $\Delta OCD$ 為等邊三角形。由此，$\angle COD = 60^\circ$。

所以，$\Delta OCD$ 的面積

$\begin{array}{cl}
= & \dfrac{1}{2} (6)(6)\sin 60^\circ \\
= & 9\sqrt{3} \mbox{ cm}^2
\end{array}$

留意

$\begin{array}{rcl}
\angle AOD+\angle BOC & = & 180^\circ – \angle COD \\
& = & 180^\circ-60^\circ \\
& = & 120^\circ
\end{array}$

所以，扇形 $OAD$ 及 扇形 $OBC$ 的面積

$\begin{array}{cl}
= & \pi(6)^2\times\dfrac{\angle AOD}{360^\circ}+\pi(6)^2\times\dfrac{\angle BOC}{360^\circ} \\
= & \pi(6)^2\times\dfrac{\angle AOD+\angle BOC}{360^\circ} \\
= & \pi(6)^2\times \dfrac{120^\circ}{360^\circ} \\
= & 12\pi \mbox{ cm}^2 \\
\end{array}$

所以，陰影部分的面積為 $(12\pi + 9\sqrt{3}) \mbox{ cm}^2$。