答案:C
因為 $\Delta CEF \sim \Delta DAF$,其中 $DF=2CF$,則可得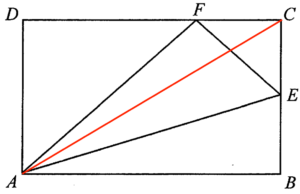
因為 $\Delta CEF \sim \Delta DAF$,其中 $DF=2CF$,則可得
$\begin{array}{rcl}
\dfrac{\Delta DAF\mbox{ 的面積}}{\Delta CEF\mbox{ 的面積}} & = & \left( \dfrac{DF}{CF}\right)^2 \\
\Delta DAF\mbox{ 的面積} & = & 2 \mbox{ cm}^2
\end{array}$
因為 $DF=2CF$,所以 $CD=3CF$。
留意 $ABCD$ 為一長方形。則 $CD=AB$。由此,$AB=3CF$。
因為 $\Delta CEF$ 及 $\Delta BEA$ 的底的長度相同,則可得
$\begin{array}{rcl}
\dfrac{\Delta CEF\mbox{ 的面積}}{\Delta BEA\mbox{ 的面積}} & = & \dfrac{CF}{BA} \\
\Delta BEA \mbox{ 的面積}& = & 3\mbox{ cm}^2
\end{array}$
連結 $AC$。

因為 $\Delta ACE$ 及 $\Delta ABE$ 的底的長度相等,且有相同的高,所以它們的面積相等。
由此 $\Delta ABC$ 的面積為 $6\mbox{ cm}^2$。
所以,長方形 $ABCD$ 的面積為 $12\mbox{ cm}^2$。
由此,$\Delta AEF$ 的面積
$\begin{array}{cl}
= & 12 – 4 – 1 – 3 \\
= & 4 \mbox{ cm}^2
\end{array}$

