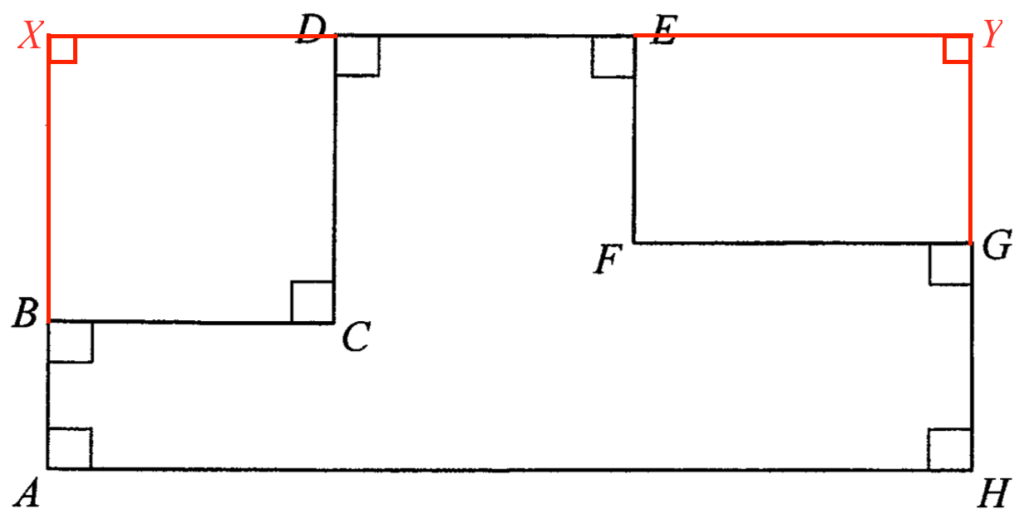
設 $X$ 為 $AB$ 及 $DE$ 的延線的交點。設 $Y$ 為 $DE$ 及 $GH$ 的延線的交點。
留意 $\angle BXD=90^\circ$ 及 $\angle GYE=90^\circ$。
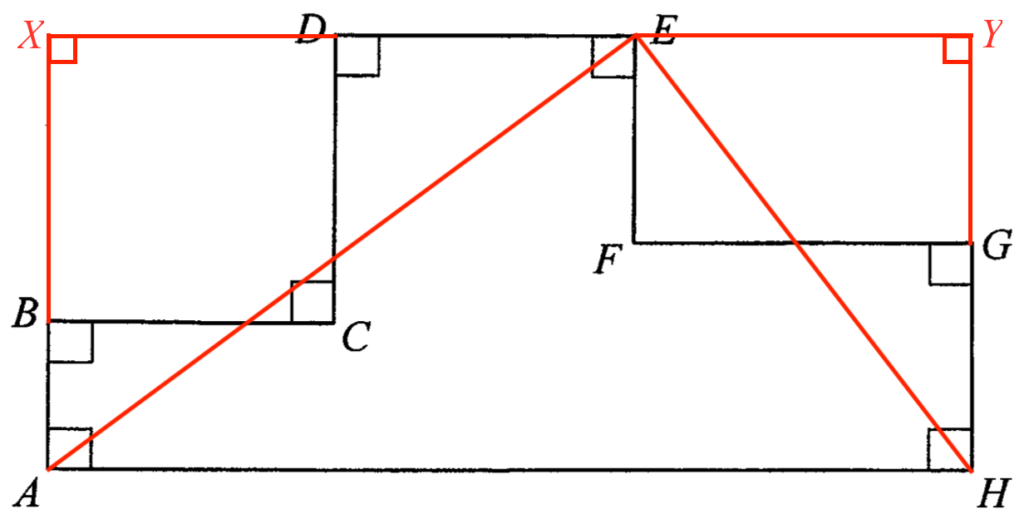
在 $\Delta AXE$ 中,
$\begin{array}{rcl}
AX & = & AB + CD \\
& = & 4 + 8 \\
& = & 12 \mbox{ cm}
\end{array}$
以及,
$\begin{array}{rcl}
XE & = & BC + DE \\
& = & 8 + 8 \\
& = & 16 \mbox{ cm}
\end{array}$
所以,可得
$\begin{array}{rcl}
AE & = & \sqrt{ AX^2+XE^2} \\
& = & \sqrt{12^2+16^2} \\
& = & 20\mbox{ cm}
\end{array}$
在 $\Delta EYH$ 中,
$\begin{array}{rcl}
EY & = & FG \\
& = & 9 \mbox{ cm}
\end{array}$
以及,
$\begin{array}{rcl}
YH & = & AX \\
& = & 12\mbox{ cm}
\end{array}$
所以,可得
$\begin{array}{rcl}
EH & = & \sqrt{EY^2+YH^2} \\
& = & \sqrt{9^2 + 12^2} \\
& = & 15 \mbox{ cm}
\end{array}$
在 $\Delta AEH$ 中,
$\begin{array}{rcl}
AH & = & BC + DE + FG \\
& = & 8 + 8 + 9 \\
& = & 25\mbox{ cm}
\end{array}$
所以 $\Delta AEH$ 的周界
$\begin{array}{cl}
= & AE + EH + AH \\
= & 20 + 15 + 25 \\
= & 60\mbox{ cm}
\end{array}$

