答案:B
在 $\Delta ABE$ 中,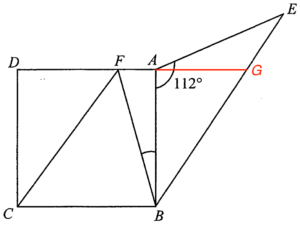
在 $\Delta ABE$ 中,
$\because AB=AE$,
$\therefore \angle ABE = \angle AEB$。
$\begin{array}{rcl}
\angle ABE & = & \dfrac{1}{2}(180^\circ-112^\circ) \\
& = & 34^\circ
\end{array}$
延長 $DA$ 使得 $DA$ 交 $BE$ 於 $G$。

留意 $FG//CB$ 及 $CF//BE$,所以 $BCFG$ 為一平行四邊形。
在 $\Delta ABG$ 中,
$\begin{array}{rcl}
\tan 34^\circ & = & \dfrac{AG}{AB} \\
AG & = & AB\tan 34^\circ
\end{array}$
因為 $AB=BC$ 及 $BC=FG$,所以 $AB=FG$。
由此在 $\Delta ABF$ 中,可得
$\begin{array}{rcl}
AF & = & FG-AG \\
& = & AB – AG \\
& = & AB – AB\tan34^\circ \\
& = & AB(1-\tan34^\circ)
\end{array}$
所以,可得
$\begin{array}{rcl}
\tan \angle ABF & = & \dfrac{AF}{AB} \\
& = & \dfrac{AB(1-\tan34^\circ)}{AB} \\
& = & 1-\tan34^\circ \\
\angle ABF & = & 18.029~627~8^\circ
\end{array}$

