答案:C
設 $AD=AF=r\mbox{ cm}$。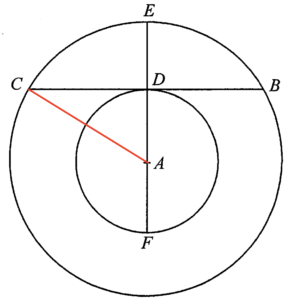
設 $AD=AF=r\mbox{ cm}$。
因為 $AD$ 為小圓的半徑及 $BC$ 為小圓於 $D$ 的切線,所以 $\angle ADC=90^\circ$。
所以,$D$ 為弦 $BC$ 的中點。由此, $CD=12\mbox{ cm}$。
連結 $A$ 及 $C$。

留意 $AE$ 及 $AC$ 為大圓的半徑,則 $AC=AE=(r+8)\mbox{ cm}$。
在 $\Delta ACD$ 中,
$\begin{array}{rcl}
AC^2 & = & AD^2 + CD^ 2 \\
(r+8)^2 & = & r^2 + 12^2 \\
16r & = & 80 \\
r & = & 5
\end{array}$
所以,
$\begin{array}{rcl}
EF & = & ED + DA + AF \\
& = & 8 + 5 + 5 \\
& = & 18 \mbox{ cm}
\end{array}$

