答案:A
考慮 $y=\tan x^\circ$ 的圖像。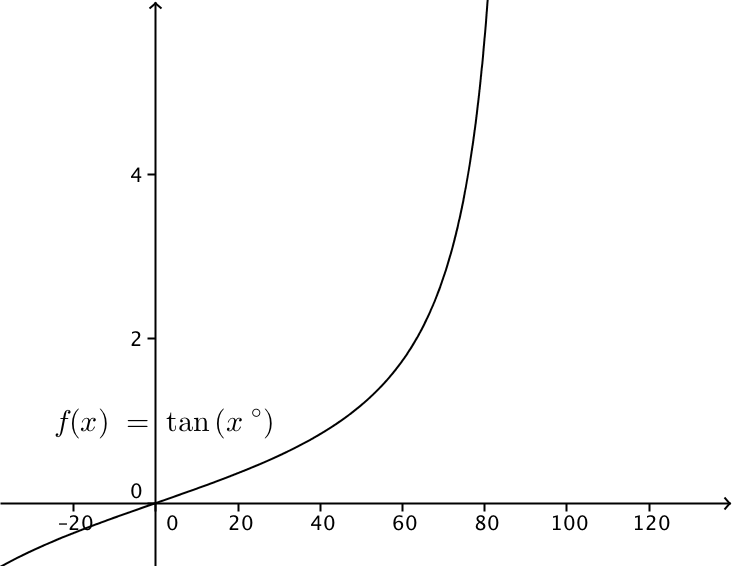
考慮 $y=\tan x^\circ$ 的圖像。

透過比較 $y=\tan x^\circ$ 及 $y=h+k\tan2x^\circ$ 兩個圖像,可知題目中的圖像經過對 $x$ 軸反射,以及向上平移 $2$ 單位。由此,$k<0$ 及 $h=2$。所以,I 及 II 為正確。
III 為錯誤。把 $x=\dfrac{\alpha^\circ}{2}$ 代入 $y=2+k\tan 2x^\circ$,可得
$\begin{array}{rcl}
y & = & 2 + k \tan (2\times\dfrac{\alpha^\circ}{2}) \\
& = & 2+k\tan \alpha^\circ
\end{array}$
若 $\tan \alpha^\circ =\dfrac{1}{k}$,則可得
$\begin{array}{rcl}
y & = & 2 + k \times\dfrac{1}{k} \\
& = & 3
\end{array}$
即圖像 $y=2+k\tan 2x^\circ$ 會通過 $(\tan \dfrac{\alpha^\circ}{2}, 3)$,所以,III 為錯誤。

