答案:D
連結 $BC$。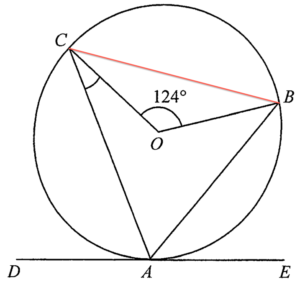
連結 $BC$。

$\begin{array}{rcl}
\angle BAC & = & \dfrac{1}{2} \times 124^\circ \\
& = & 62^\circ
\end{array}$
因為 $AB$ 為 $\angle CAE$ 的角平分線,可得
$\begin{array}{rcl}
\angle BAE & = & \angle BAC \\
& = & 62^\circ
\end{array}$
因為 $DE$ 為圓於點 $A$ 的切線,可得
$\begin{array}{rcl}
\angle ACB & = & \angle BAE \\
& = & 62^\circ
\end{array}$
在 $\Delta OBC$ 中,
$\because OC = OB$,
$\therefore \angle OCB = \angle OBC$。
由此,可得
$\begin{array}{rcl}
\angle OCB & = & \dfrac{1}{2} (180^\circ – 124^\circ) \\
& = & 28^\circ
\end{array}$
所以,可得
$\begin{array}{rcl}
\angle ACO & = & \angle ACB – \angle OCB \\
& = & 62^\circ – 28^\circ \\
& = & 34^\circ
\end{array}$

