答案:D
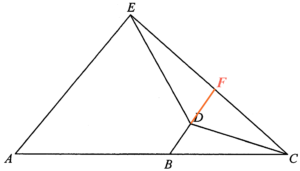

延長 $BD$,使 $BD$ 交 $EC$ 於 $F$。留意 $BF//AE$ 及 $\Delta ACE \sim \Delta BCF$,可得
$\begin{array}{rcl}
AC:BC & = & EC:FC \\
& = & 5:2
\end{array}$
所以,$EF:FC = 3:2$。
若以 $CF$ 及 $EF$ 分別為 $\Delta CDF$ 及 $\Delta EDF$ 的底,兩個三角形便會有相同的高。所以 $\Delta CDF$
$\begin{array}{cl}
= & 8 \times \dfrac{2}{3+2} \\
= & 3.2 \text{ cm}^2
\end{array}$
由於 $\Delta ACE \sim \Delta BCF$,可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta BCF$ 的面積}}{\text{$\Delta ACE$ 的面積}} & = & \left(\dfrac{BC}{AC}\right)^2 \\
\dfrac{3.2 + 4}{\text{$\Delta ACE$ 的面積}} & = & \left(\dfrac{2}{5}\right)^2 \\
\text{$\Delta ACE$ 的面積} & = & 45 \text{ cm}^2
\end{array}$
由此,梯形 $ABDE$ 的面積
$\begin{array}{cl}
= & 45 – 4 – 8 \\
= & 33 \text{ cm}^2
\end{array}$

