答案:D
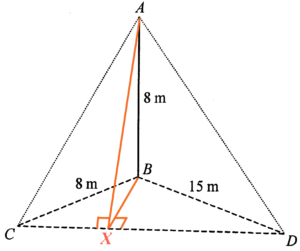

留意 $\angle AXB = \theta$。考慮 $\Delta BCD$,根據畢氐定理,可得
$\begin{array}{rcl}
CD & = & \sqrt{8^2 + 15^2} \\
& = & 17
\end{array}$
由此,可得
$\begin{array}{rcl}
\sin \angle BCD & = & \dfrac{15}{17}
\end{array}$
考慮 $\Delta BCX$,
$\begin{array}{rcl}
\sin \angle BCD & = & \dfrac{BX}{8} \\
BX & = & 8 \sin \angle BCD \\
BX & = & 8 \times \dfrac{15}{17} \\
BX & = & \dfrac{120}{17}
\end{array}$
考慮 $\Delta ABX$,
$\begin{array}{rcl}
\tan \theta & = & \dfrac{AB}{BX} \\
\tan \theta & = & \dfrac{8}{ \frac{120}{17}} \\
\tan \theta & = & \dfrac{17}{15}
\end{array}$

