2015-I-19

1. 在 $\Delta ABC$ 運用餘弦公式，可得

   $\begin{array}{rcl}
   AC^2 & = & AB^2 + BC^2 – 2(AB)(AC)\cos \angle ABC \\
   AC^2 & = & (40)^2 + (24)^2 -2(40)(24) \cos \angle 80^\circ \\
   AC & = & 42.925\ 464\ 46
   \end{array}$

   所以，$A$ 至 $C$ 的距離為 $42.9\text{ cm}$。

2. 在 $\Delta ABC$ 運用正弦公式，可得

   $\begin{array}{rcl}
   \dfrac{AB}{\sin \angle ACB} & = & \dfrac{AC}{\sin \angle ABC} \\
   \dfrac{40}{\sin \angle ACB} & = & \dfrac{42.925\ 464\ 46}{\sin 80^\circ} \\
   \sin \angle ACB & = & \dfrac{40\sin 80^\circ}{42.925\ 464\ 46} \\
   \sin \angle ACB & = & 0.917\ 690\ 926 \\
   \angle ACB & = & 66.590\ 814\ 87^\circ \\
   \angle ACB & \approx & 66.6^\circ
   \end{array}$

3. 連結 $AC$ 及 $AD$。
   

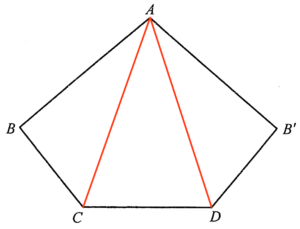
   明顯地該紙卡分為三部分：$\Delta ABC$、$\Delta ACD$ 及 $\Delta AB’D$。由於 $AB=AB’=40$、$BC= B’D=24$ 及 $\angle ABC = \angle AB’D=80^\circ$，所以 $\Delta ABC \cong \Delta AB’D$。$\Delta ABC$ 的面積

   $\begin{array}{cl}
   = & \dfrac{1}{2} \times AB \times BC \times \sin \angle ABC \\
   = & \dfrac{1}{2} \times 40 \times 24 \times \sin 80^\circ \\
   = & 480\sin80^\circ \text{ cm}^2
   \end{array}$

   由於 $AC=AD$，則 $\Delta ACD$ 的面積

   $\begin{array}{cl}
   = & \dfrac{1}{2} \times AC \times AD \times \sin \angle CAD \\
   = & \dfrac{1}{2} \times 42.925\ 464\ 46^2 \times \sin \angle CAD \\
   = & 921.297\ 749\ 4 \sin \angle CAD \text{ cm}^2
   \end{array}$

   所以，該紙卡的面積

   $\begin{array}{cl}
   = & 2 \times 480 \sin 80^\circ + 921.297\ 749\ 4 \sin \angle CAD \\
   = & 960 \sin 80^\circ + 921.297\ 749\ 4 \sin \angle CAD
   \end{array}$

   由此，$\sin \angle CAD$ 的值越大，該紙卡的面積越大。

   留意 $AC=AD$，則 $\angle ACD = \angle ADC$。

   $\begin{array}{rcl}
   \angle CAD & = & 180^\circ – 2 \times \angle ACD \\
   \angle CAD & = & 180^\circ – 2 \times (\angle BCD – \angle ACB) \\
   \angle CAD & = & 180^\circ – 2\angle BCD + 2(66.590\ 814\ 87^\circ) \\
   \angle CAD & = & 313.181\ 629\ 7^\circ – 2\angle BCD
   \end{array}$

   由於 $105^\circ \le \angle BCD \le 145^\circ$，則可得

   $23.181\ 629\ 74^\circ \le \angle CAD \le 103.181\ 629\ 7^\circ$。

   所以，$\sin \angle CAD$ 的值在 $\angle CAD = 90^\circ$ 時為最大。由此，該紙卡的面積在 $\angle CAD = 90^\circ$ 時為最大。若 $\angle CAD = 90^\circ$，$\angle ACD = 45^\circ$。所以，該紙卡的面積在 $\angle BCD$

   $\begin{array}{cl}
   = & 45^\circ + \angle ACB \\
   = & 45^\circ + 66.590\ 814\ 87^\circ \\
   = & 111.590\ 814\ 9^\circ
   \end{array}$

   時為最大。

   由此，我們可下此結論：

   當 $\angle BCD$ 由 $105^\circ$ 增加至 $111.590\ 814\ 9^\circ$，該紙卡的面積會隨之增加。當 $\angle BCD$ 由 $111.590\ 814\ 9^\circ$ 增加至 $145^\circ$，該紙卡的面積會隨之減少。

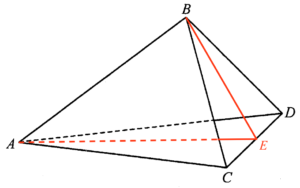
考慮 $\Delta ACE$，

$\begin{array}{rcl}
\angle ACD & = & \angle BCD – \angle ACB \\
\angle ACD & = & 132^\circ – 66.590\ 814\ 87^\circ \\
\angle ACD & = & 65.409\ 185\ 513^\circ
\end{array}$

由於 $AC=AD$ 及 $E$ 為 $CD$ 的中點，則 $\angle AEC$ 為一直角。由此，可得

$\begin{array}{rcl}
\cos \angle ACE & = & \dfrac{CE}{AC} \\
CE & = & AC \cos \angle ACE \\
CE & = & 42.925\ 464\ 46 \cos 65.409\ 185\ 513^\circ \\
CE & = & 17.862\ 789\ 29 \text{ cm}
\end{array}$

及

$\begin{array}{rcl}
\sin \angle ACE & = & \dfrac{AE}{AC} \\
AE & = & AC \sin \angle ACE \\
AE & = & 42.925\ 464\ 46 \sin 65.409\ 185\ 513^\circ \\
AE & = & 39.032\ 246\ 38\text{ cm}
\end{array}$

考慮 $\Delta BCE$。由於 $BC = BD$ 及 $E$ 為 $CD$ 的中點，則 $\angle BEC$ 為一直角。在 $\Delta BCD$ 中運用畢氏定理，可得

$\begin{array}{rcl}
BE^2 & = & BC^2 – CE^2 \\
BE & = & \sqrt{24^2 – (17.862\ 789\ 29)^2} \\
BE & = & 16.028\ 747\ 88 \text{ cm}
\end{array}$

考慮 $\Delta ABE$。在 $\Delta ABE$ 中運用餘弦公式，可得

$\begin{array}{rcl}
\cos \angle AEB & = & \dfrac{AE^2 + BE^2 – AB^2}{2(AE)(BE)} \\
\cos \angle AEB & = & 0.144\ 202\ 402 \\
\angle AEB & = & 81.708\ 905\ 17^\circ
\end{array}$

設 $X$ 為 $B$ 在平面 $ACD$ 上的垂足。由於 $\Delta ABC \cong \Delta ABD$，則 $X$ 在 $AE$ 之上。

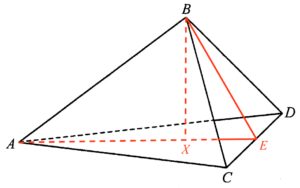
考慮 $\Delta BXE$。留意 $\angle BXE$ 為一直角。由此，可得

$\begin{array}{rcl}
\sin \angle BEX & = & \dfrac{BX}{BE} \\
BX & = & BE \sin \angle BEX \\
BX & = & 16.028\ 747\ 88 \sin 81.708\ 905\ 17^\circ \\
BX & = & 15.861\ 218\ 83 \text{ cm}
\end{array}$

所以，角錐體 $ABCD$ 的體積

$\begin{array}{cl}
= & \dfrac{1}{3} \times \text{ the area of $\Delta ACD$} \times BX \\
= & \dfrac{1}{3} \times \dfrac{1}{2} \times CD \times AE \times BX \\
= & 3686.278\ 337 \text{ cm}^3 \\
\approx & 3690 \text{ cm}^3
\end{array}$