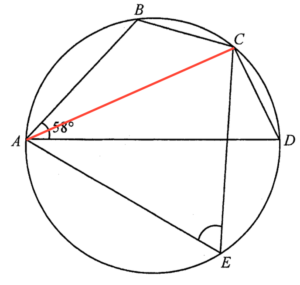
連結 $AC$。
$\begin{array}{ll}
BC = CD & \text{(已知)} \\
\overparen{BC} = \overparen{CD} & \text{(等弦對等弧)} \\
\angle BAC = \angle CAD & \text{(弧長與圓心角成比例)}
\end{array}$
所以,可得
$\begin{array}{rcl}
\angle CAD & = & \dfrac{1}{2} \times \angle BAD \\
\angle CAD & = & \dfrac{1}{2} \times 58^\circ \\
\angle CAD & = & 29^\circ
\end{array}$
由於 $AD$ 為圓的一直徑,可得
$\begin{array}{ll}
\angle ACD = 90^\circ & \text{(半圓上的圓周角)} \\
\end{array}$
在 $\Delta ACD$ 中,
$\begin{array}{rcll}
\angle ADC & = & 180^\circ – \angle ACD – \angle CAD & \text{($\Delta$ 的內角和)} \\
\angle ADC & = & 180^\circ – 90^\circ – 29^\circ \\
\angle ADC & = & 61^\circ
\end{array}$
由於 $A$、$C$、$D$ 及 $E$ 為圓周上的四點,可得
$\begin{array}{rcll}
\angle AEC & = & \angle ADC & \text{(同弓形內的圓周角)} \\
\angle AEC & = & 61^\circ
\end{array}$

