2016-I-20

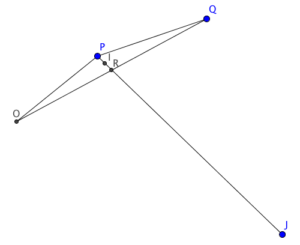
考慮 $\Delta PRO$ 及 $\Delta PRQ$。

由於 $I$ 為 $\Delta OPQ$ 的內心，則 $PI$ 為 $\angle OPQ$ 的角平分線。由此，可得

$\begin{array}{ll}
\angle RPO = \angle RPQ & \text{(內心)}
\end{array}$

由於 $J$ 為 $\Delta OPQ$ 的外心，則 $PJ$ 為 $OQ$ 的垂直平分線。由此，可得

$\begin{array}{ll}
\angle PRO = \angle PRQ = 90^\circ & \text{(外心)} \\
RO = RQ & \text{(外心)}
\end{array}$

所以，$\Delta PRO \cong \Delta PRQ$ (A.A.S)。由此，可得

$\begin{array}{ll}
OP = PQ & \text{($\cong \Delta$ 的對應邊)}
\end{array}$

1. 參考下圖。
   

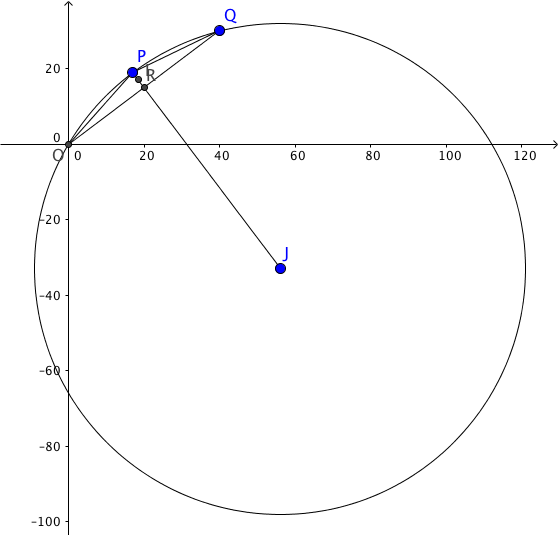
   設 $P=(a, 19)$。利用 (a) 的結果，$OP=PQ$。由此，可得

   $\begin{array}{rcl}
   \sqrt{(a-0)^2 + (19-0)^2} & = & \sqrt{(a-40)^2 + (19-30)^2} \\
   a^2 + 361 & = & a^2 -80a + 1721 \\
   80a & = & 1360 \\
   a & = & 17
   \end{array}$

   設 $x^2+y^2+Dx+Ey+F=0$ 為 $C$ 的方程。由於 $C$ 通過 $O$、$P$ 及 $Q$，可得

   $\left\{ \begin{array}{ll}
   (0)^2 + (0)^2 +D(0) + E(0) + F =0 & \ldots \unicode{x2460} \\
   17^2 + 19^2 + D(17) + E(19) + F = 0 & \ldots \unicode{x2461} \\
   40^2 + 30^2 +D(40) + E(30) + F = 0 & \ldots \unicode{x2462}
   \end{array} \right.$

   從 $\unicode{x2460}$，可得 $F=0$。把 $\unicode{x2461}$ 及 $\unicode{x2462}$ 化簡後，可得

   $\left\{ \begin{array}{ll}
   17D + 19E + 650 =0 & \ldots \unicode{x2463} \\
   40D + 30E + 2500 = 0 & \ldots \unicode{x2464}
   \end{array} \right.$

   $\unicode{x2463} \times 30 – \unicode{x2464} \times 19$，可得

   $\begin{array}{rcl}
   -250D -28000 & = & 0 \\
   D & = & -112
   \end{array}$

   把 $D=-112$ 代入 $\unicode{x2463}$，可得

   $\begin{array}{rcl}
   17(-112) + 19E + 650 & = & 0 \\
   19E & = & 1254 \\
   E & = & 66
   \end{array}$

   由此，$C$ 的方程為 $x^2 +y^2 -112x +66y=0$。

2. 參考下圖 。
   

   設 $y=\dfrac{3}{4}x + c$ 為 $C$ 的切線，其中斜率為 $\dfrac{3}{4}$。把 $y= \dfrac{3}{4}x +c$ 代入 $C$ 的方程，可得

   $\begin{array}{rcl}
   x^2 + (\dfrac{3}{4}x+c)^2 -112x +66(\dfrac{3}{4}x+c) & = & 0 \\
   x^2 + \dfrac{9}{16}x^2 + \dfrac{3c}{2}x +c^2 -112x + \dfrac{99}{2} x + 66c & = & 0 \\
   16x^2 + 9x^2 + 24cx + 16c^2 – 1792x + 792 x + 1056c & = & 0 \\
   25x^2 + (24c-1000)x + (16c^2 + 1056c) & = & 0
   \end{array}$

   由於 $y=\dfrac{3}{4}x +c$ 為 $C$ 的切線，可得

   $\begin{array}{rcl}
   \Delta & = & 0 \\
   (24c-1000)^2 – 4(25)(16c^2 +1056c) & = & 0 \\
   576c^2 – 48000c + 1000000 – 1600c^2 – 105600c & = & 0 \\
   1024c^2 + 153600c – 1000000 & = & 0 \\
   16c^2 + 2400c – 15625 & = & 0 \\
   (4c -25)(4c+625) & = & 0
   \end{array}$

   所以，$c=\dfrac{25}{4}$ 或 $c=\dfrac{-625}{4}$。

   所以，$L_1$ 及 $L_2$ 的方程分別為 $y=\dfrac{3}{4}x + \dfrac{25}{4}$ 及 $y=\dfrac{3}{4}x -\dfrac{625}{4}$。由此，$S$、$T$、$U$ 及 $V$ 的坐標分別為 $(\dfrac{-25}{3},0)$、$(0,\dfrac{25}{4})$、$(\dfrac{625}{3},0)$ 及 $(0,\dfrac{-625}{4})$。

   留意梯形 $STUV$ 的高為圓 $C$ 的直徑。則梯形 $STUV$ 的高

   $\begin{array}{cl}
   = & \sqrt{(\dfrac{112}{2})^2 + (\dfrac{66}{2})^2 – 0} \\
   = & 65
   \end{array}$

   所以，梯形 $STUV$ 的面積

   $\begin{array}{cl}
   = & \dfrac{2\times 65}{2} \left[ \sqrt{(\dfrac{-25}{3}-0)^2 + (0-\dfrac{25}{4})^2} + \sqrt{(\dfrac{625}{3} – 0)^2 + (0- \dfrac{-625}{4})^2} \right] \\
   = & \dfrac{105625}{6} \\
   > & 17000
   \end{array}$

   所以，該宣稱正確。