2016-II-15

答案：B
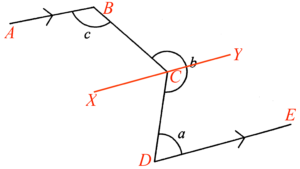
在圖中加入通過 $C$ 點的直線 $DE$，使得 $AB\text{//}XY\text{//}DE$。

I 不一定正確。

$\angle BCY = c$ (錯角，$AB$//$XY$)

$\angle XCD = a$ (錯角，$XY$//$DE$)

若 $\angle BCX = a$，則可得

$a + c = 180^\circ$ (直線上的鄰角)。

可是，$\angle BCX$ 不一定等於 $a$。所以 I 不一定正確。

II 必為正確。

$\angle BCY = c$ (錯角，$AB$//$XY$)

$\angle XCD = a$ (錯角，$XY$//$DE$)

$\begin{array}{cl}
& a + b – c \\
= & \angle XCD + \text{反角 } BCD – \angle BCY \\
= & \angle XCY \\
= & 180^\circ
\end{array}$

由此，II 必為正確。

III 不一定正確。

$\angle BCX = 180^\circ- c$ (同旁內角，$AB$//$XY$)

$\angle XCD = a$ (錯角，$XY$//$DE$)

若 $a = 2c + 180^\circ$，則可得

$\begin{array}{rcl}
\angle BCD & = & 180^\circ – c + a \\
\angle BCD & = & 180^\circ – c + (2c +180^\circ) \\
\angle BCD & = & c
\end{array}$

所以，

$b + c = 360^\circ$ (同頂角)

可是，$a$ 不一定等於 $2c + 180^\circ$。

由此，III 不一定正確。