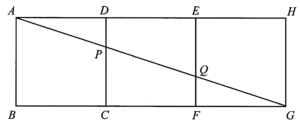
由於 $ABCD$、$CDEF$ 及 $EFGH$ 均為正方形,可得 $AD:DE:EH = 1: 1:1$ 及 $BC: CF:FG=1:1:1$。
由於 $\Delta ADP \sim \Delta AEQ$,則可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta ADP$ 的面積}}{\text{$\Delta AEQ$ 的面積}} & = & \left( \dfrac{AD}{AE} \right)^2 \\
\dfrac{\text{$\Delta ADP$ 的面積}}{\text{$\Delta AEQ$ 的面積}} & = & \left( \dfrac{1}{2} \right)^2 \\
\dfrac{\text{$\Delta ADP$ 的面積}}{\text{$\Delta AEQ$ 的面積}} & = & \dfrac{1}{4}
\end{array}$
由此,可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta ADP$ 的面積}}{\text{四邊形 $DEQP$ 的面積}} & = & \dfrac{1}{3} \\
\end{array}$
由於 $\Delta ADP \sim \Delta AHG$,則可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta ADP$ 的面積}}{\text{$\Delta AHG$ 的面積}} & = & \left( \dfrac{AD}{AH} \right)^2 \\
\dfrac{\text{$\Delta ADP$ 的面積}}{\text{$\Delta AHG$ 的面積}} & = & \left( \dfrac{1}{3} \right)^2 \\
\dfrac{\text{$\Delta ADP$ 的面積}}{\text{$\Delta AHG$ 的面積}} & = & \dfrac{1}{9}
\end{array}$
由此,可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta ADP$ 的面積}}{\text{四邊形 $DHGP$ 的面積}} & = & \dfrac{1}{8} \\
\end{array}$
所以,可得
$\begin{array}{rcl}
\dfrac{\text{四邊形 $DEQP$ 的面積}}{\text{四邊形 $DHGP$ 的面積}} & = & \dfrac{3}{8} \\
\dfrac{\text{四邊形 $DEQP$ 的面積}}{\text{四邊形 $EHGQ$ 的面積}} & = & \dfrac{3}{5} \\
\end{array}$
由於四邊形 $ABCP$ 的面積 $=$ 四邊形 $EHGQ$ 的面積,可得
$\begin{array}{rcl}
\dfrac{\text{四邊形 $DEQP$ 的面積}}{\text{四邊形 $ABCP$ 的面積}} & = & \dfrac{3}{5} \\
\end{array}$

