答案:D
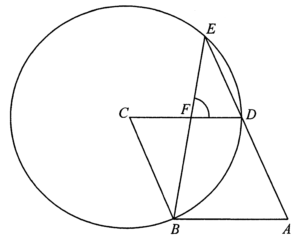

由於 $ABCD$ 為一菱形,$BC\text{//}AD$。
$\begin{array}{rcll}
\angle BCD + \angle ADC & = & 180^\circ & \text{(同旁內角,$BC$//$AD$)} \\
\angle BCD + 118^\circ & = & 180^\circ & \\
\angle BCD & = & 62^\circ
\end{array}$
由此,可得
$\begin{array}{rcll}
\angle BED & = & \dfrac{1}{2} \times \angle BCD & \text{(圓心角兩倍於圓周角)} \\
\angle BED & = & \dfrac{1}{2} \times 62^\circ & \\
\angle BED & = & 31^\circ & \\
\end{array}$
考慮 $\Delta DEF$,可得
$\begin{array}{rcll}
\angle DEF & = & \angle ADC – \angle BED & \text{($\Delta$ 的外角)} \\
\angle DEF & = & 118^\circ – 31^\circ & \\
\angle DEF & = & 87^\circ
\end{array}$

