2017-I-12

$\begin{array}{cl}
= & \text{角柱體的體積} \\
= & 84 \times 20 \\
= & 1\ 680 \text{ cm}^3
\end{array}$

由於兩角錐體相似，可得

$\begin{array}{rcl}
\dfrac{\text{較小角錐體的體積}}{\text{較大角錐體的體積}} & = & \left(\sqrt{\dfrac{4}{9}} \right)^3 \\
& = & \dfrac{8}{27}
\end{array}$

由此，較大角錐體的體積

$\begin{array}{cl}
= & 1\ 680 \times \dfrac{27}{27+8} \\
= & 1\ 296 \text{ cm}^3
\end{array}$

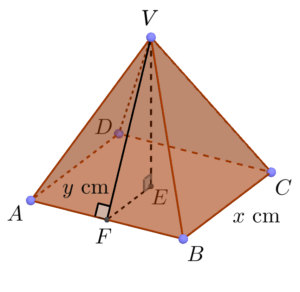
留意 $VE$ 為較大角錐體的高，則 $E$ 為 $V$ 的垂足。也留意 $VF$ 為 $\Delta VAB$ 的高。

設 $x\text{ cm}$ 為較大角錐體的底的邊長。利用 (a) 的結果，可得

$\begin{array}{rcl}
\dfrac{1}{3} \times x^2 \times 12 & = & 1\ 296 \\
x & = & 18
\end{array}$

設 $y\text{ cm}$ 為 $VF$ 的長度。考慮 $\Delta VEF$，可得

$\begin{array}{rcll}
VF^2 & = & FE^2 + VE^2 & \text{(畢氏定理)} \\
y^2 & = & 9^2 + 12^2 & \\
y & = & \sqrt{225} & \\
y & = & 15
\end{array}$

所以，$\Delta VAB$ 的面積

$\begin{array}{cl}
= & \dfrac{1}{2} \times 18 \times 15 \\
= & 135 \text{ cm}^2
\end{array}$

所以，較大角錐體的總表面面積

$\begin{array}{cl}
= & 4 \times 135 + 18^2 \\
= & 864 \text{ cm}^2
\end{array}$

由此，可得

$\begin{array}{rcl}
\dfrac{\text{較小角錐體的總表面面積}}{\text{較大角錐體的總表面面積}} & = & \dfrac{4}{9} \\
\dfrac{\text{較小角錐體的總表面面積}}{864} & = & \dfrac{4}{9} \\
\text{較小角錐體的總表面面積} & = & 384 \text{ cm}^2
\end{array}$