- 在 $\Delta ABC$ 運用正弦公式,可得
$\begin{array}{rcl}
\dfrac{AC}{\sin \angle ABC} & = & \dfrac{BC}{\sin \angle BAC} \\
\dfrac{AC}{\sin (180^\circ – 30^\circ-42^\circ)} & = & \dfrac{24}{\sin 30^\circ} \\
AC & = & 45.650\ 712\ 78 \text{ cm}
\end{array}$- 連結 $D$、$E$ 及 $F$。留意 $DEF$ 為一直線。
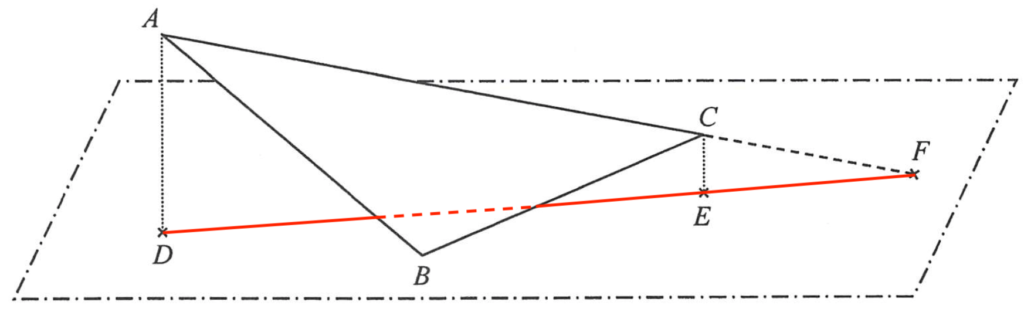
由於 $D$ 及 $E$ 均為水平地面上的點,且分別鉛垂於頂點 $A$ 及頂點 $C$ 之下,則 $\Delta ADF \sim \Delta CEF$。所以,可得
$\begin{array}{rcl}
\dfrac{AD}{CD} & = & \dfrac{AF}{CF} \\
\dfrac{10}{2} & = & \dfrac{AC + CF}{CF} \\
10 CF & = & 2AC + 2CF \\
8CF & = & 2AC \\
CF & = & 11.412\ 678\ 2\text{ cm}
\end{array}$ - 留意 $\Delta ABC$ 的高與 $\Delta ABF$ 的高相等。所以 $\Delta ABF$ 的高
$\begin{array}{cl}
= & BC \times \sin \angle BCA \\
= & 24 \times \sin 42^\circ \text{ cm}
\end{array}$$\therefore \Delta ABF$ 的面積
$\begin{array}{cl}
= & \dfrac{1}{2} \times AF \times \Delta ABF \text{ 的高} \\
= & \dfrac{1}{2}\times ( 45.650\ 712\ 78 + 11.412\ 678\ 2) \times (24 \times \sin 42^\circ) \\
= & 458.194\ 336\ 9\text{ cm}^2
\end{array}$ - 連結 $FB$。延長 $FB$ 至點 $X$ 使得 $AX \perp FB$ 及 $DX \perp FB$。
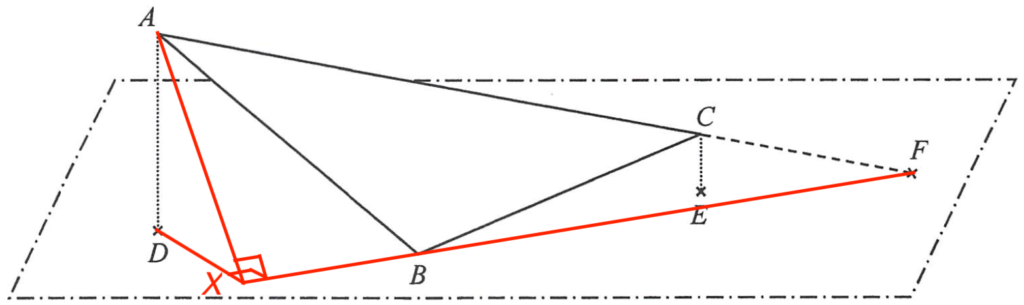
留意所求的角為 $\angle AXD$。
在 $\Delta BCF$ 運用餘弦公式,可得
$\begin{array}{rcl}
BF^2 & = & CF^2 +BC^2 -2(BC)(BF)\cos \angle BCF \\
BF^2 & = & (11.412\ 678\ 2)^2 +24^2 – 2(11.412\ 678\ 2)(24) \cos (180^\circ – 42^\circ) \\
BF & = & 33.366\ 904\ 449\text{ cm}
\end{array}$留意當以 $BF$ 為底時,$AX$ 為 $\Delta ABF$ 的高。所以利用 (b)(ii) 的結果,可得
$\begin{array}{rcl}
\dfrac{1}{2} \times AX \times BF & = & \Delta ABF\text{ 的面積} \\
\dfrac{1}{2} \times AX \times 33.366\ 904\ 449 & = & 458.194\ 336\ 9 \\
AX & = & 27.464\ 000\ 26 \text{ cm}
\end{array}$考慮 $\Delta ADX$,
$\begin{array}{rcl}
\sin \angle AXD & = & \dfrac{AD}{AX} \\
\sin \angle AXD & = & \dfrac{10}{27.464\ 000\ 26} \\
\angle AXD & = & 21.353\ 006\ 46^\circ
\end{array}$所以,金屬薄片 $ABC$ 與水平地面間的傾角為 $21.4^\circ$。
- 連結 $BD$ 及 $DF$。
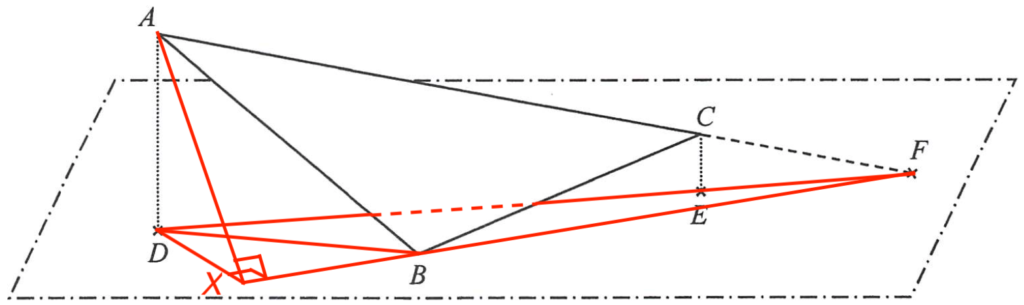
留意當以 $BF$ 為底時,$DX$ 為 $\Delta BDF$ 的高。所以 $\Delta BDF$ 的面積
$\begin{array}{cl}
= & \dfrac{1}{2} \times DX \times BF \\
= & \dfrac{1}{2} \times \dfrac{AD}{\tan \angle AXD} \times BF \\
= & \dfrac{1}{2} \times \dfrac{10}{\tan 21.353\ 006\ 46^\circ} \times 33.366\ 904\ 449 \\
= & 426.741\ 482\text{ cm}^2 \\
< & 460\text{ cm}^2 \end{array}$由此,我不同意該工匠的宣稱。
- 連結 $D$、$E$ 及 $F$。留意 $DEF$ 為一直線。
2017-I-19
答案:(a) $45.7\text{ cm}$ (b) (i) $11.4\text{ cm}$ (ii) $458\text{ cm}^2$ (iii) $21.4^\circ$ (iv) 不同意

