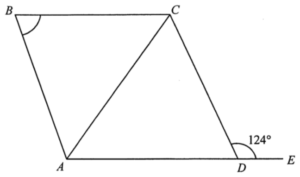
考慮 $\Delta ACD$,
$\begin{array}{rcl}
\angle ADC & = & 180^\circ – 124^\circ \ \text{(直線上的鄰角)} \\
\angle ADC & = & 56^\circ
\end{array}$
由於 $AC = AD$,可得
$\begin{array}{rcl}
\angle ACD & = & \angle ADC \ \text{(等腰 $\Delta$ 的底角)} \\
\angle ACD & = & 56^\circ
\end{array}$
所以,可得
$\begin{array}{rcl}
\angle CAD & = & 180^\circ – \angle ADC – \angle ACD \ \text{($\Delta$ 的內角和)} \\
\angle CAD & = & 180^\circ – 56^\circ – 56^\circ \\
\angle CAD & = & 68^\circ
\end{array}$
由於 $AE\text{//}BC$,則可得
$\begin{array}{rcl}
\angle BCA & = & \angle CAD \ \text{(錯角,$AE$//$BC$)} \\
\angle BCA & = & 68^\circ
\end{array}$
考慮 $\Delta ABC$。由於 $AB=BC$,可得
$\begin{array}{rcl}
\angle BAC & = & \angle BCA \ \text{(等腰 $\Delta$ 的底角)} \\
\angle BAC & = & 68^\circ
\end{array}$
所以,可得
$\begin{array}{rcl}
\angle ABC & = & 180^\circ – \angle BAC – \angle BCA \ \text{($\Delta$ 的內角和)} \\
\angle ABC & = & 180^\circ – 68^\circ – 68^\circ \\
\angle ABC & = & 44^\circ
\end{array}$

