加通過 $A$ 的直線 $XZ$ 使得 $XZ \perp GH$ 及 $XZ \perp FE$。$XZ$ 交 $CD$ 於 $Y$ 且 $XZ \perp CD$。$AB$ 延線分別交 $GF$ 及 $DE$ 於 $P$ 及 $Q$。留意 $PQ \perp GF$ 及 $PQ \perp DE$。
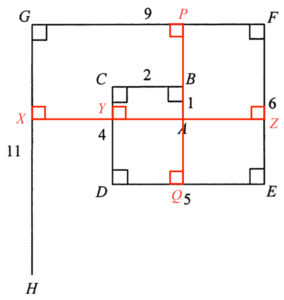
由於 $ABCY$ 為一長方形,則 $CY = AB = 1$。由此,可得
$\begin{array}{rcl}
DY & = & CD – CY \\
DY & = & 4 -1 \\
DY & = & 3
\end{array}$
由於 $DEZY$ 為一長方形,則 $DY = EZ = 3$。由此,可得
$\begin{array}{rcl}
FZ & = & EF – EZ \\
FZ & = & 6 – 3 \\
DY & = & 3
\end{array}$
由此 $XZFG$ 為一長方形,則 $FZ = GX = 3$。由此,可得
$\begin{array}{rcl}
XH & = & GH – GX \\
XH & = & 11 – 3 \\
XH & = & 8
\end{array}$
由於 $BCDQ$ 為一長方形,則 $BC = DQ = 2$。由此,可得
$\begin{array}{rcl}
QE & = & DE – DQ \\
QE & = & 5 – 2 \\
QE & = & 3
\end{array}$
由於 $PQEF$ 為一長方形,則 $QE = PF = 3$。由此,可得
$\begin{array}{rcl}
GP & = & GF – PF \\
GP & = & 9 – 3 \\
GP & = & 6
\end{array}$
由於 $PGXA$ 為一長方形,則 $GP = XA = 6$。
在 $\Delta AXH$ 中運用畢氏定理,可得
$\begin{array}{rcl}
AH^2 & = & XH^2 + XA^2 \\
AH^2 & = & (8)^2 + (6)^2 \\
AH^2 & = & 100 \\
AH & = & 10
\end{array}$

