根據題目的條件,作圖如下。
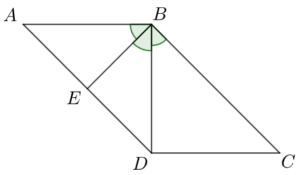
I 為正確。由於 $ABCD$ 為一平行四邊形,則 $AD//BC$。
在 $\Delta EBD$,
$\angle BDA = \angle DBC$ (錯角,$AD//DC$)
$\therefore EB=ED$ (等角對等邊)
在 $\Delta EBA$,
$ED = EA$ ($E$ 為 $AD$ 的中點)
$\therefore EA = EB$。
由此,可得 $\angle EAB = \angle EBA$ (等腰 $\Delta$ 的底角)。
在 $\Delta BAD$,
$\because \angle BAD = \angle ABE$、$\angle ABE = \angle CBD$ 及 $\angle CBD = \angle BDE$,
$\therefore \angle BAD = \angle BDA$。
$\therefore AB = BD$ (等角對等邊)。
II 為正確。由於 $\angle ABE = \angle DBE = \angle CBD = \angle BAD$ 及 $AD//BC$,可得
$\begin{array}{rcll}
\angle BAD + \angle ABC & = & 180^\circ & \text{(同旁內角,$AD//BC$)} \\
\angle BAD + \angle ABE + \angle DBE + \angle CBD& = & 180^\circ \\
4\angle ABE & = & 180^\circ \\
\angle ABE & = & 45^\circ \\
\end{array}$
所以,可得
$\begin{array}{rcl}
\angle ABC & = & 3 \times \angle ABE \\
& = & 3 \times 45^\circ \\
& = & 135^\circ
\end{array}$
III 為正確。在 $\Delta ABE$ 及 $\Delta DBE$ 中,
$\begin{array}{rcll}
BE & = & BE & \text{(公共邊)} \\
AB & = & DB & \text{(已證)} \\
AE & = & DE & \text{($E$ 為 $AD$ 的中點)}
\end{array}$
$\therefore \Delta ABD \cong \Delta DBE$ (S.S.S.)。

