2018-I-18

對於 $f(2) = 60$，可得

$\begin{array}{rcl}
k_1 (2)^2 + k_2(2) & = & 60 \\
2k_1 + k_2 & = & 30 \ \ldots \unicode{x2460}
\end{array}$

對於 $f(3) = 99$，可得

$\begin{array}{rcl}
k_1(3)^2 + k_2(3) & = & 99 \\
3k_1 + k_2 & = & 33 \ \ldots \unicode{x2461}
\end{array}$

$\unicode{x2461} – \unicode{x2460}$，可得

$\begin{array}{rcl}
k_1 & = & 3
\end{array}$

把 $k_1 = 3$ 代入 $\unicode{x2460}$，可得

$\begin{array}{rcl}
2(3) + k_2 & = & 30 \\
k_2 & = & 24
\end{array}$

所以，$f(x) = 3x^2 + 24x$。

1. 利用 (a) 的結果，可得

   $\begin{array}{rcl}
   f(x) & = & 3x^2 + 24x \\
   & = & 3(x^2 + 8x) \\
   & = & 3\left[x^2 + 8x + \left(\dfrac{8}{2}\right)^2 – \left(\dfrac{8}{2}\right)^2\right] \\
   & = & 3(x + 4)^2 – 48
   \end{array}$

   所以，$Q$ 的坐標為 $(-4, -48)$。

2. 留意 $y= 27 – f(x)$ 代表把 $f(x)$ 對 $x$ 軸反射，之後再向上平移 $27$ 單位。所以 $Q$ 及 $R$ 的 $x$ 坐標相同，而 $R$ 的 $y$ 坐標

   $\begin{array}{cl}
   = & 27 – \text{$Q$ 的 $y$ 坐標} \\
   = & 27 – (-48) \\
   = & 75
   \end{array}$

   所以，$R$ 的坐標為 $(-4, 75)$。

3. 根據題目的資訊略繪以下的圖像。
   

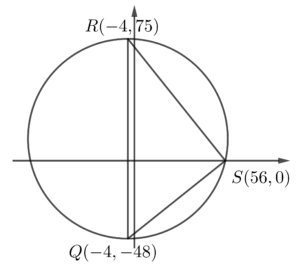
   考慮 $\Delta QRS$。

   $\begin{array}{rcl}
   RS^2 + QS^2 & = & (56-(-4)^2 + (0-75)^2 + (56-(-4))^2 + (0-(-48))^2 \\
   & = & 15129
   \end{array}$

   另外，

   $\begin{array}{rcl}
   RQ^2 & = & (75-(-48))^2 \\
   & = & 15129
   \end{array}$

   由於 $RS^2 + QS^2 = RQ^2$，根據畢氏定理的逆定理， $\Delta QRS$ 為一直角三角形，其中 $\angle QSR =90^\circ$，

   由於 $\angle QSR = 90^\circ$，根據半圓上的圓周角的逆定理，$QR$ 為該圓的直徑。

   由於 $P$ 為 $\Delta QRS$ 的外心，則 $P$ 為 $QR$ 的中點。