2019-I-17

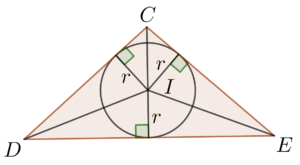
留意三角形的周界 $p = CD + DE + CE$。

也留意 $CD$、$DE$ 及 $CE$ 均為該圓的切線。所以根據半徑 $\perp$ 切線定理，$r$ 為 $\Delta CDI$、$\Delta DEI$ 及 $\Delta CEI$ 的高。由此，可得

$\begin{array}{rcl}
a & = & \dfrac{1}{2} \times CD \times r + \dfrac{1}{2} \times DE \times r + \dfrac{1}{2} \times CD \times r \\
2a & = & r(CD + DE + CE) \\
2a &= & pr \\
pr & = & 2a
\end{array}$

1. 由於 $P$ 與 $OH$ 及 $HK$ 等距，所以 $\Gamma$ 為 $\angle OHK$ 的角平分線。
2. 設 $I(h,k)$ 為 $\Delta OHK$ 的內心。
   

   $\begin{array}{rcl}
   OH & = & \sqrt{9^2 + 12^2} \\
   & = & 15 \\
   HK & = & \sqrt{(9-14)^2 + ( 12 -0)^2} \\
   & = & 13 \\
   OK & = & 14 – 0 \\
   OK & = & 14
   \end{array}$

   $\Delta OHK$ 的面積

   $\begin{array}{cl}
   = & \dfrac{1}{2} \times OK \times \text{$H$ 的 $y$ 坐標} \\
   = & \dfrac{1}{2} \times 14 \times 12 \\
   = & 84
   \end{array}$

   由於 $OK$ 為 $\Delta OHK$ 的內切圓的切線，則 $I$ 的 $y$ 坐標為該圓的半徑。利用 (a) 的結果，可得

   $\begin{array}{rcl}
   (OH + OK + HK) \times k & = & 2 \times \text{$\Delta OHK$ 的面積} \\
   k & = & \dfrac{2 \times 84}{13 + 14 + 15} \\
   k & = & 4
   \end{array}$

   考慮 $\angle HOK$。

   $\begin{array}{rcl}
   \tan \angle HOK & = & \dfrac{12 – 0}{9 – 0} \\
   \angle HOK & = & \tan^{-1} \dfrac{4}{3}
   \end{array}$

   考慮 $\angle IOK$。

   $\begin{array}{rcl}
   \angle IOK & = & \dfrac{1}{2} \times \angle HOK \\
   \tan \angle IOK & = & \tan \dfrac{1}{2} \times \angle HOK \\
   \dfrac{4 – 0}{h – 0} & = & \tan \left(\dfrac{1}{2} \times \tan^{-1} \dfrac{4}{3}\right) \\
   \dfrac{4}{h} & = & \dfrac{1}{2} \\
   h & = & 8
   \end{array}$

   所以，$\Gamma$ 的方程為

   $\begin{array}{rcl}
   \dfrac{y – 12}{x – 9} & = & \dfrac{4 – 12}{8 – 9} \\
   y – 12 & = & 8x – 72 \\
   8x – y – 60 & = & 0
   \end{array}$