2020-I-17

所以，$y = g(x)$ 圖像的頂點的坐標為 $(k, k^2 + 4)$。

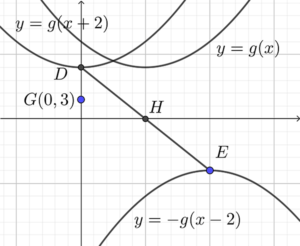
留意 $D$ 及 $E$ 的坐標分別為 $(k-2,k^2 +4)$ 及 $(k+2, -k^2 – 4)$。

對於 $\Delta DEF$ 的外接圓，$DE$ 為該圓的弦。由此， $DE$ 的垂直平分線必定通過 $\Delta DEF$ 的外心。設 $H$ 為 $DE$ 的中點及 $G=(0,3)$。

$DE$ 的斜率

$\begin{array}{cl}
= & \dfrac{(k^2 + 4) – (-k^2 -4)}{(k-2) – (k+2)} \\
= & \dfrac{-(k^2 + 4)}{2}
\end{array}$

$H$ 的坐標

$\begin{array}{cl}
= & \left(\dfrac{(k-2) + (k+2)}{2}, \dfrac{(k^2+4) + (-k^2 -4)}{2} \right) \\
= & (k, 0)
\end{array}$

$GH$ 的斜率

$\begin{array}{cl}
= & \dfrac{0 – 3}{k – 0} \\
= & \dfrac{-3}{k}
\end{array}$

由於 $GH \perp DE$，可得

$\begin{array}{rcl}
\dfrac{-3}{k} \times \dfrac{-(k^2 + 4)}{2} & = & -1 \\
3k^2 + 12 & = & -2k \\
3k^2 +2k + 12 & = & 0
\end{array}$

考慮 $3k^2 + 2k +12 =0$ 的判別式，可得

$\begin{array}{rcl}
\Delta & = & (2)^2 – 4(3)(12) \\
& = & -140 \\
& < & 0 \end{array}$

所以，方程 $3k^2 + 2k + 12 = 0$ 沒有實根。

所以，在同一直角坐標系內，沒有一點 $F$ 使得 $\Delta DEF$ 的外心的坐標為 $(0,3)$。