2020-I-19

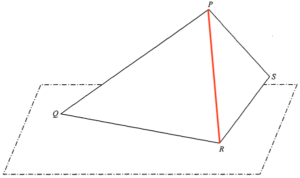
在 $\Delta PQR$ 運用正弦公式，可得

$\begin{array}{rcl}
\dfrac{PR}{\sin \angle PQR} & = & \dfrac{PQ}{\sin \angle PRQ} \\
\dfrac{PR}{\sin 30^\circ} & = & \dfrac{60}{\sin 55^\circ} \\
PR & = & 36.623\ 237\ 66^\circ
\end{array}$

另外，

$\begin{array}{rcll}
\angle QPR & = & 180^\circ – 30^\circ – 55^\circ & \text{($\Delta$ 的內角和)} \\
\angle QPR & = & 95^\circ
\end{array}$

在 $\Delta PRS$ 運餘弦公式，可得

$\begin{array}{rcl}
RS^2 & = & PS^2 + PR^2 – 2\times PS \times PR \times \cos \angle RPS \\
RS^2 & = & 40^2 + 36.623\ 237\ 66^2 – 2 \times 40 \times 36.623\ 237\ 66 \times \cos (120^\circ – 95^\circ) \\
RS & = & 16.908\ 799\ 44\text{ cm}
\end{array}$

$\begin{array}{cl}
= & \dfrac{1}{2} \times PQ \times PR \times \sin \angle QPR + \dfrac{1}{2} \times PR \times PS \times \sin \angle RPS \\
= & \dfrac{1}{2} \times 60 \times 36.623\ 237\ 66 \times \sin 95^\circ + \dfrac{1}{2} \times 36.623\ 237\ 66 \times 40 \times \sin 25^\circ \\
= & 1404.069\ 236 \text{ cm}^2
\end{array}$

1. 設 $P’$ 為 $P$ 在該水平地面的投影，$M$ 為 $P$ 在 $QR$ 的垂足。
   

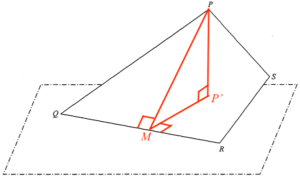
   考慮 $\Delta PMQ$。

   $\begin{array}{rcl}
   \sin \angle PQM & = & \dfrac{PM}{PQ} \\
   \sin 30^\circ & = & \dfrac{PM}{60} \\
   PM & = & 30\text{ cm}
   \end{array}$

   由於該紙卡與水平地面的交角為 $32^\circ$，則 $\angle PMP’ = 32^\circ$。

   $\begin{array}{rcl}
   \sin \angle PMP’ & = & \dfrac{PP’}{PM} \\
   \sin 32^\circ & = & \dfrac{PP’}{30} \\
   PP’ & = & 15.897\ 577\ 93 \text{ cm}
   \end{array}$

   所以，$P$ 至水平地面的最短距離為 $15.9\text{ cm}$。

2. 設 $S’$ 為 $S$ 在水平地面的投影，$N$ 為 $PS$ 的延線與 $P’S’$ 的延線的交點。
   

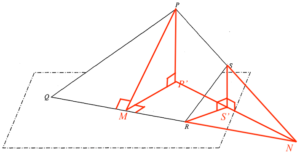
   考慮 $\Delta PQN$。

   $\begin{array}{rcll}
   \angle PNQ & = & 180^\circ – 30^\circ – 120^\circ & \text{($\Delta$ 的內角和)} \\
   \angle PNQ & = & 30^\circ \\
   \therefore PQ & = & PN & \text{(等腰 $\Delta$ 的底角)}
   \end{array}$

   留意 $\Delta PNP’ \sim SNS’$。可得

   $\begin{array}{rcll}
   \dfrac{SS’}{PP’} & = & \dfrac{SN}{PN} & \text{($\sim \Delta$ 的對應邊)} \\
   \dfrac{SS’}{PP’} & = & \dfrac{PN – PS}{PN} \\
   \dfrac{SS’}{15.897\ 577\ 93} & = & \dfrac{60 – 40}{60} \\
   SS’ & = & 5.299\ 192\ 642 \text{ cm}
   \end{array}$

   留意 $RS$ 與水平地面的交角為 $\angle SRS’$。考慮 $\Delta SRS’$。

   $\begin{array}{rcl}
   \sin \angle SRS’ & = & \dfrac{SS’}{RS} \\
   \sin \angle SRS’ & = & \dfrac{5.299\ 192\ 642}{16.908\ 799\ 44} \\
   \angle SRS’ & = & 18.264\ 160\ 68^\circ \\
   \angle SRS’ & \le & 20^\circ
   \end{array}$

   所以，該宣稱正確。