連結 $DG$。
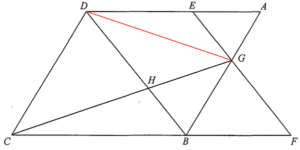
考慮 $\Delta AEG$ 及 $\Delta DEG$。若分別以 $AE$ 及 $DE$ 為底的話,它們的高會相等。所以,可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta DEG$ 的面積}}{\text{$\Delta AEG$ 的面積}} & = & \dfrac{DE}{AE} \\
\dfrac{\text{$\Delta DEG$ 的面積}}{48} & = & \dfrac{5}{2} \\
\text{$\Delta DEG$ 的面積} & = & 120 \text{ cm}^2
\end{array}$
由於 $BF = DE$ 及 $AD//CF$,則 $BFED$ 為一平行四邊形。由此,可得 $EG//DB$。
由於,$EG//DB$,則 $\Delta AEG \sim \Delta ADB$。由此,可得
$\begin{array}{rcl}
AG : GB & = & AE : ED \\
AG : GB & = & 2 : 5
\end{array}$
由於 $ABCD$ 為一平行四邊形,則 $AB = DC$。由此,可得
$\begin{array}{rcl}
AG : GB : DC & = & AG : GB : AB \\
AG : GB : DC & = & 2 : 5 : 7
\end{array}$
考慮 $\Delta ADG$ 及 $\Delta CDG$。若分別以 $AG$ 及 $CD$ 為底的話,它們的高會相等。所以,可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta CDG$ 的面積}}{\text{$\Delta ADG$ 的面積}} & = & \dfrac{CD}{AG} \\
\dfrac{\text{$\Delta DEG$ 的面積}}{48 + 120} & = & \dfrac{7}{2} \\
\text{$\Delta DEG$ 的面積} & = & 588 \text{ cm}^2
\end{array}$
由於 $ABCD$ 為一平行四邊形,則 $AB // DC$。由此,可得 $\Delta BGH \sim \Delta DCH$。所以
$\begin{array}{rcl}
\dfrac{CH}{GH} & = & \dfrac{CG}{GB} \\
\dfrac{CH}{GH} & = & \dfrac{7}{5}
\end{array}$
考慮 $\Delta CDH$ 及 $\Delta DGH$。若分別以 $CH$ 及 $GH$ 為底的話,它們的高會相等。所以,可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta CDH$ 的面積}}{\text{$\Delta DGH$ 的面積}} & = & \dfrac{CH}{GH} \\
\dfrac{\text{$\Delta CDH$ 的面積}}{\text{$\Delta DGH$ 的面積}} & = & \dfrac{7}{5}
\end{array}$
由此,$\Delta CDH$ 的面積
$\begin{array}{cl}
= & \text{$\Delta CDG$ 的面積} \times \dfrac{7}{7 + 5} \\
= & 588 \times \dfrac{7}{12} \\
= & 343 \text{ cm}^2
\end{array}$

