2020-II-21

答案：C
在 $\Delta BCE$ 中，

$\begin{array}{cl}
& BE^2 + BC^2 \\
= & 8^2 + 15^2 \\
= &289
\end{array}$

另外，

$\begin{array}{cl}
& BC^2 \\
= & 17^2 \\
= & 289
\end{array}$

由於 $BE^2 + CE^2 = BC^2$，則根據畢氏定理的逆定理，$\Delta BCE$ 為一直角三角形，其中 $\angle BEC = 90^\circ$。

由此，可得

$\begin{array}{rcl}
\cos \angle EBC & = & \dfrac{BE}{BC} \\
\cos \angle EBC & = & \dfrac{8}{17} \\
\angle EBC & = & 61.927\ 513\ 06^\circ
\end{array}$

在 $BC$ 上加點 $F$ 使得 $EF \perp BC$。

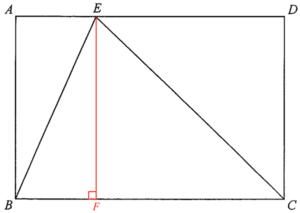
考慮 $\Delta BEF$。

$\begin{array}{rcl}
\sin angle EBF & = & \dfrac{EF}{BE} \\
EF & = & 8 \times \sin 61.927\ 513\ 06^\circ \\
EF & = & 7.058\ 823\ 529 \text{ cm}
\end{array}$

所以，長方形 $ABCD$ 的面積

$\begin{array}{cl}
= & BC \times EF \\
= & 17 \times 7.058\ 823\ 529 \\
= & 120 \text{ cm}^2
\end{array}$