略繪該不等式組如下。
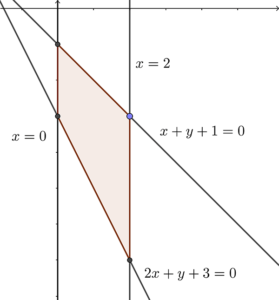
把 $x=0$ 代入 $x+y+1=0$,可得
$\begin{array}{rcl}
0 + y + 1 & = & 0 \\
y & = & -1
\end{array}$
所以,該交點為 $(0,-1)$。
把 $x=2$ 代入 $x+y+1=0$,可得
$\begin{array}{rcl}
2 + y + 1 & = & 0 \\
y & = & -3
\end{array}$
所以,該交點為 $(2,-3)$。
把 $x=0$ 代入 $2x+y+3=0$,可得
$\begin{array}{rcl}
2(0) + y + 3 & = & 0 \\
y & = & -3
\end{array}$
所以,該交點為 $(0,-3)$。
把 $x=2$ 代入 $2x+y+3=0$,可得
$\begin{array}{rcl}
2(2) + y + 3 & = & 0 \\
y & = & -7
\end{array}$
所以,該交點為 $(2,-7)$。
在 $(0,-1)$,
$\begin{array}{cl}
& 4(0) + 3(-1) +k \\
= & k-3
\end{array}$
在 $(2,-3)$,
$\begin{array}{cl}
& 4(2) + 3(-3) +k \\
= & k-1
\end{array}$
在 $(0,-3)$,
$\begin{array}{cl}
& 4(0) + 3(-3) +k \\
= & k-9
\end{array}$
在 $(2,-7)$,
$\begin{array}{cl}
& 4(2) + 3(-7) +k \\
= & k-13
\end{array}$
明顯地,$4x + 3y + k$ 的極小值為 $k-13$。所以,可得
$\begin{array}{rcl}
k – 13 & = & 24 \\
k & = & 37
\end{array}$

