2020-M2-06

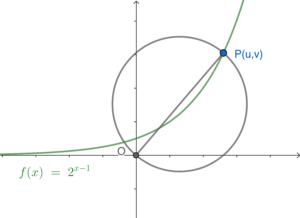
利用距離公式，可得 $OP=\sqrt{u^2+v^2}$。

設 $A$ 平方單位為以 $OP$ 為直徑之圓的面積。由此，可得

$\begin{array}{rcl}
A & = & \pi \left(\dfrac{OP}{2} \right)^2 \\
A & = & \pi \left( \dfrac{\sqrt{u^2+v^2}}{2} \right)^2 \\
A & = & \dfrac{\pi(u^2+v^2)}{4} \\
A & = & \dfrac{\pi S}{4} \\
\dfrac{dA}{dt} & = & \dfrac{\pi}{4} \times \dfrac{dS}{dt} \\
5\pi & = & \dfrac{\pi}{4} \times \dfrac{dS}{dt} \\
\dfrac{dS}{dt} & = & 20 \text{ , 此為常數。}
\end{array}$

所以，$S$ 為恒速增加。

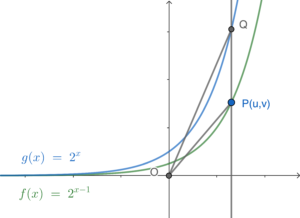
留意 $Q$ 的 $y$ 坐標為 $2^u$。

設 $B$ 平方單位為 $\Delta OPQ$ 的面積。由此，可得

$\begin{array}{rcl}
B & = & \dfrac{1}{2} \times \text{$P$ 的 }x \text{ 坐標} \times PQ \\
B & = & \dfrac{1}{2} \times u \times (2^u-2^{u-1}) \\
B & = & u(2^{u-1}-2^{u-2}) \\
B & = & u( 2\times 2^{u-2}-2^{u-2}) \\
B & = & u2^{u-2} \\
\dfrac{dB}{dt} & = & 2^{u-2}\times \dfrac{du}{dt} +u \times 2^{u-2} \times \ln 2 \times \dfrac{du}{dt}\\
\dfrac{dB}{dt} & = & (1+u\ln 2)2^{u-2} \dfrac{du}{dt}
\end{array}$

利用 (a) 的結果，可得

$\begin{array}{rcl}
\dfrac{dS}{dt} & = & 20 \\
\dfrac{d}{dt}(u^2+v^2) & = & 20 \\
\dfrac{d}{dt}(u^2+(2^{u-1})^2) & = & 20 \\
2u\dfrac{du}{dt}+2(2^{u-1}) \times 2^{u-1} \ln2 \times \dfrac{du}{dt} & = & 20 \\
2u\dfrac{du}{dt} +2(2^{u-1})^2\ln2\dfrac{du}{dt} & = & 20
\end{array}$

當 $u=2$ 時，可得

$\begin{array}{rcl}
2(2)\dfrac{du}{dt}+2(2^{2-1})^2\ln 2\dfrac{du}{dt} & = & 20 \\
\dfrac{du}{dt} (4-8\ln2) & = & 20 \\
\dfrac{du}{dt} & = & \dfrac{5}{1+2\ln2}
\end{array}$

由此，當 $u=2$ 時，可得

$\begin{array}{rcl}
\dfrac{dB}{dt} & = & (1+2\ln2)2^{2-2} \times \dfrac{5}{1+2\ln2} \\
\dfrac{dB}{dt} & = & 5
\end{array}$

所以，所求的變率為每秒 $5$ 平方單位。