答案:(a) $10$ (b) 是 (c) $120$
- $G$ 的圓心
$\begin{array}{cl}
= & \left( -\dfrac{-12}{2}, -\dfrac{-16}{2}\right) \\
= & (6, 8)
\end{array}$$\therefore OG$
$\begin{array}{cl}
= & \sqrt{(6-0)^2+(8-0)^2} \\
= & 10
\end{array}$ - 把 $(0,0)$ 代入圓 $C$ 的方程的左方,可得
$\begin{array}{cl}
& 0^2 + 0^2 -12(0) -16(0) – 69 \\
= & -69 \\
< & 0 \end{array}$$\therefore O$ 在圓 $C$ 之內。
- 參考下圖。設 $F$ 為 $OG$ 的中點。
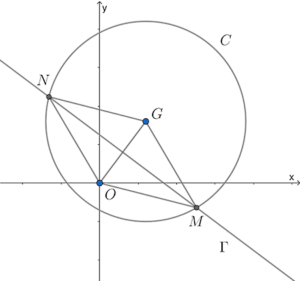
圓的半徑
$\begin{array}{cl}
= & \sqrt{(6)^2+(8)^2 -(-69)} \\
= & 13
\end{array}$考慮 $\Delta FGN$,
$\begin{array}{rcll}
NF^2 & = & NG^2 – FG^2 & \text{(畢氏定理)} \\
NF^2 & = & 13^2 – (\dfrac{10}{2})^2 \\
NF^2 & = & 144 \\
NF & = & 12
\end{array}$$\therefore$ 四邊形 $OMGN$ 的面積
$\begin{array}{cl}
= & 2 \times \dfrac{1}{2} \times OG \times NF \\
= & 10 \times 12 \\
= & 120
\end{array}$

