2021-I-16

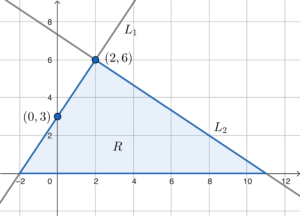
$L_1$ 的方程為

$\begin{array}{rcl}
\dfrac{y-6}{x-2} & = & \dfrac{3-6}{0-2} \\
2y-12 & = & 3x-6 \\
3x -2y +6 & = & 0
\end{array}$

把 $(0,0)$ 代入 $3x -2y +6=0$ 的左方，可得

$\begin{array}{cl}
& 3(0) -2(0) + 6 \\
= & 6 \\
\ge & 0
\end{array}$

由於 $(0,0)$ 在 $R$ 內，則其中一個不等式為 $3x -2y +6 \ge 0$。

由於 $L_1 \perp L_2$，則 $L_2$ 的斜率

$\begin{array}{cl}
= & -1 \div m_{L_1} \\
= & -1 \div \dfrac{3}{2} \\
= & \dfrac{-2}{3}
\end{array}$

由此，$L_2$ 的方程為

$\begin{array}{rcl}
\dfrac{y-6}{x-2} & = & \dfrac{-2}{3} \\
3y-18 & = & -2x +4 \\
2x +3y -22 & = & 0
\end{array}$

把 $(0,0)$ 代入 $2x+3y-22=0$ 的左方，可得

$\begin{array}{cl}
& 2(0) +3(0) -22 \\
= & -22 \\
\le & 0
\end{array}$

由於 $(0,0)$ 在 $R$ 內，則其中一個不等式為 $2x +3y -22 \le 0$。

由於 $R$ 在 $x$ 的上方，則其中一個不等式為 $y\ge 0$。

由此，該不等式組為 $\left\{ \begin{array}{l} 3x -2y +6 \ge 0 \\ 2x +3y -22 \le 0 \\ y \ge 0 \end{array} \right.$。

在頂點 $(-2,0)$，

$\begin{array}{cl}
& 8(-2) -5(0) \\
= & -16
\end{array}$

在頂點 $(2,6)$，

$\begin{array}{cl}
& 8(2)-5(6) \\
= & -14
\end{array}$

在頂點 $(11,0)$，

$\begin{array}{cl}
& 8(11) -5(0) \\
= & 88
\end{array}$

$\therefore 8x-5y$ 在 $R$ 內的極小值為 $-16$。