-
$\begin{array}{rcl}
f(x) & = & x^2 -12kx -14x +36k^2 +89k +53 \\
& = & x^2 -(12k +14)x +36k^2 +89k +53 \\
& = & x^2 -(12k +14)x +(6k +7)^2 -(6k +7)^2 +36k^2 +89k +53 \\
& = & [x -(6k+7)]^2 -36k^2 -84k -49 +36k^2 +89k +53 \\
& = & [x -(6k+7)]^2 +5k +4
\end{array}$$\therefore Q$ 的坐標為 $(6k +7, 5k +4)$。
- 留意 $y=f(14-x)=f(-(x-14))$。由此,$y=f(x)$ 會先向右平移 $14$ 單位,然後再對 $y$ 軸反射。
由此,頂點的坐標先平移至 $(6k +7 -14, 5k +4) = (6k -7, 5k +4)$,然後反射至 $(-(6k-7), 5k+4) = (7-6k, 5k+4)$。所以,$R$ 的坐標為 $(7 -6k, 5k +4)$。
- 依題意略繪下圖。(為了略繪下圖,在此假定 $k=2$。)
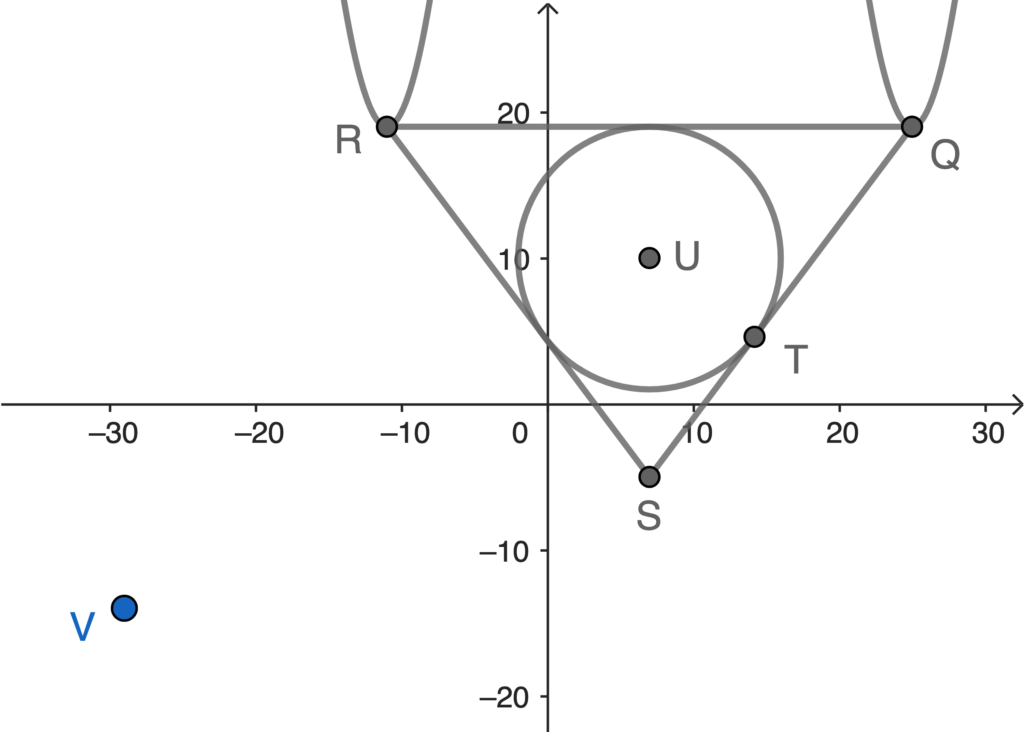
- 通過 $Q$ 及 $S$ 的直線的方程為
$\begin{array}{rcl}
\dfrac{y-(4-3k)}{x-7} & = & \dfrac{5k +4 -(4-3k)}{6k +7 -7} \\
\dfrac{y +3k -4}{x -7} & = & \dfrac{4}{3} \\
3y +9k -12 & = & 4x -28 \\
4x -3y -9k -16 & = & 0
\end{array}$ - 留意 $Q$ 及 $R$ 的 $y$ 坐標相同。所以 $QR$ 為一水平線。
考慮 $Q$、$R$ 及 $S$ 的 $x$ 坐標。
$\begin{array}{rcl}
\dfrac{1}{2} (\text{$Q$ 的 $x$ 坐標} +\text{$R$ 的 $x$ 坐標}) & = & \dfrac{1}{2}(6k +7 + 7 -6k) \\
& = &7 \\
& = & \text{$S$ 的 $x$ 坐標}
\end{array}$所以,$\Delta QRS$ 為一等腰三角形,其中 $SQ = SR$。
設 $r$ 為 $\Delta QRS$ 內切圓 $C$ 的半徑。則 $C$ 的圓心為 $(7, 5k +4 -r)$。
由此,$C$ 的方程為 $(x -7)^2 +(y -5k -4 +r)^2 = r^2$。
$\left\{ \begin{array}{l}
(x -7)^2 +(y -5k -4 +r)^2 = r^2 & \ldots \unicode{x2460} \\
4x -3y -9k -16 = 0 & \ldots \unicode{x2461}
\end{array}\right.$從 $\unicode{x2461}$,可得
$\begin{array}{rcl}
4x -3y -9k -16 & = & 0 \\
y & = & \dfrac{4x -16 -9k}{3} \ldots \unicode{x2462}
\end{array}$把 $\unicode{x2462}$ 代入 $\unicode{x2460}$,可得
$\begin{array}{rcl}
(x -7)^2 + \left(\dfrac{4x -16 -9k}{3} -5k -4 +r \right)^2 & = & r^2 \\
x^2 -14x +49 +\dfrac{1}{9}(4x -16 -9k -15k -12 +3r)^2 -r^2 & = & 0 \\
9x^2 -126x +441 +(4x -28 -24k +3r)^2 -9r^2 & = & 0 \\
9x^2 -126x +441 +16x^2 +784 +576k^2 +9r^2 -224x \ \ \ \ \ & & \\
-192kx +24rx +1344k -168r -144kr -9r^2 & = & 0 \\
25x^2 +(24r-192k-350)x +(576k^2 -144kr +1344k -168r +1225) & = & 0 \\
\end{array}$由於 $QS$ 為 $C$ 於 $T$ 的切線,則可得
$\begin{array}{rcl}
\Delta & = & 0 \\
(24r -192k -350)^2 -4(25)(576k^2 -144kr +1344k -168r +1225) & = & 0 \\
576r^2 +36864k^2+ 122500 -9216kr -16800r +134400k \ \ \ \ \ & & \\
-57600k^2 +14400kr -134400k +16800r -122500 & = & 0\\
576r^2 -5184kr +36864k^2 & = & 0 \\
r^2 +9kr -36k^2 & = & 0 \\
(r-3k)(r+12k) & = & 0
\end{array}$$\therefore r=3k$ 或 $r=-12k$ (拾去)。
由此,$C$ 的方程為
$\begin{array}{rcl}
(x -7)^2 +(y-5k-4+3k)^2 & = & (3k)^2 \\
(x-7)^2 +(y -2k -4)^2 & = & 9k^2
\end{array}$ - 對於 $ST\text{//}VU$,
$\begin{array}{rcl}
m_{ST} & = & m_{VU} \\
m_{QS} & = & m_{VU} \\
\dfrac{4}{3} & = & \dfrac{-14 -(2k+4)}{-29 -7} \\
-144 & = & -54 -6k\\
k & = & 15
\end{array}$所以,當 $k=15$ 時 $ST\text{//}VU$。
當 $k=15$ 時,該圖像變為
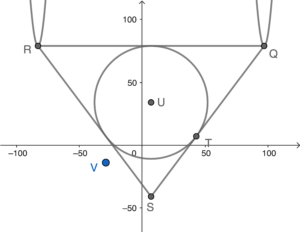
另外,$S$ 及 $U$ 的坐標分別為 $(7,-41)$ 及 $(7,34)$。
$SV$ 的斜率
$\begin{array}{cl}
= & \dfrac{-14+41}{-29 -7} \\
= & \dfrac{-3}{4}
\end{array}$由於 $m_{SV} \times m_{TS}=-1$,則 $SV\perp TS$。
由於 $ST$ 為 $C$ 在 $T$ 的切線,且 $UT$ 為一半徑,則 $UT \perp ST$。
由於 $SV\perp TS$ 及 $UT \perp ST$,則 $SV\text{//}TU$。
所以當 $k=15$ 時,$ST\text{//}VU$ 及 $SV\text{//}TU$。所以 $STUV$ 為一平行四邊形。
由於 $STUV$ 為一平行四邊形,且 $UT\perp ST$ (即 $\angle UTS =90^\circ$),則 $STUV$ 為一長方形。
所以,$STUV$ 有可能為一長方形。
- 通過 $Q$ 及 $S$ 的直線的方程為
2021-I-19
答案:(a) $(6k+7,5k+4)$ (b) $(7-6k,5k+4)$ (c) (i) $4x-3y-9k-16=0$ (ii) $(x-7)^2+(y-2k-4)^2=9k^2$ (iii) 有可能

