答案:C

設 $C$ 為圓心。則 $C$ 的坐標
$\begin{array}{cl}
= & \left( -\dfrac{-18}{2}, -\dfrac{-20}{2} \right) \\
= & (9, 10)
\end{array}$
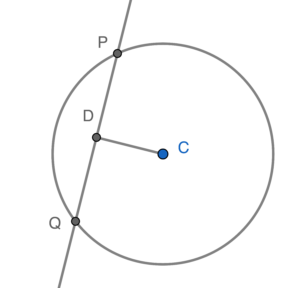
把 $PQ$ 的中點記為 $D(s,t)$。由於 $D$ 為 $PQ$ 的中點,則 $CD \perp PQ$ (圓心至弦中點的連線垂直弦)。由此,可得
$\begin{array}{rcl}
m_{CD} \times m_{PQ} & = & -1 \\
\dfrac{t-10}{s-9} \times 4 & = & -1 \\
4t-40 & = & -s+9 \\
s+4t-49 & = & 0
\end{array}$

