答案:(a) $20$ (b) (i) $GH$ 與 $GP$ 互相垂直。 (ii) $220$
- $G$ 的坐標
$\begin{array}{cl}
= & \left( -\dfrac{-154}{2}, -\dfrac{-128}{2} \right) \\
= & (77, 64)
\end{array}$所以,$G$ 與 $H$ 的距離
$\begin{array}{cl}
= & \sqrt{(77-65)^2 +(64-48)^2} \\
= & 20
\end{array}$ - 依題意略繪下圖。
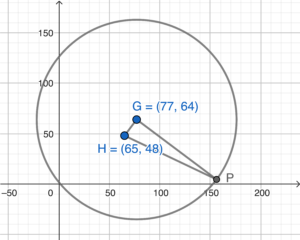
- 對於 $\Delta GHP$ 的面積為最大,$GP$ 必須為半徑,且 $\angle HGP =90^\circ$。所以,$GH$ 與 $GP$ 互相垂直。
- 留意 $GP$ 為 $C$ 的半徑。可得
$\begin{array}{rcl}
GP & = & \sqrt{77^2+64^2-224} \\
GP & = & 99
\end{array}$在 $\Delta GHP$ 中,
$\begin{array}{rcll}
HP^2 & = & HG^2 +GP^2 & \text{(畢氏定理)} \\
HP & = & \sqrt{20^2 +99^2} \\
HP & = & 101
\end{array}$所以,$\Delta GHP$ 的周界
$\begin{array}{cl}
= & 20 + 99 + 101 \\
= & 220
\end{array}$

