答案:(a) $(-2k,4k^2+8)$ (b) $(-k,5k^2+10)$
-
$\begin{array}{rcl}
g(x) & = & 3x^2+12kx+16k^2+8 \\
g(x) & = & 3(x^2 +4kx) +16k^2 +8 \\
g(x) & = & 3(x^2 +4kx +(2k)^2 -(2k)^2) +16k^2 +8 \\
g(x) & = & 3[(x+2k)^2 -4k^2] +16k^2 +8 \\
g(x) & = & 3(x+2k)^2 -12k^2 +16k^2 +8 \\
g(x) & = & 3(x+2k)^2 +4k^2 +8
\end{array}$所以,該頂點的坐標為 $(-2k, 4k^2 +8)$。
- 依題意略繪下圖,在此假定 $k=\dfrac{-3}{2}$。
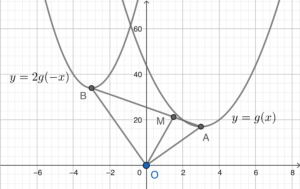
留意 $y=2g(-x)$ 的圖像是先把 $y=g(x)$ 對 $y$ 反射,然後再沿 $y$ 軸放大至原來的 $2$ 倍。
所以,$B$ 的坐標為 $(2k, 8k^2+16)$。
也留意若 $\Delta OBM$ 及 $\Delta OAM$ 分別以 $BM$ 及 $AM$ 為底的話,它們有相同的高。所以,可得
$\begin{array}{cl}
& AM : BM \\
= & \text{$\Delta OAM$ 的面積} : \text{$\Delta OBM$ 的面積} \\
= & 1 : 3
\end{array}$由此,$M$ 的坐標
$\begin{array}{cl}
= & \left( \dfrac{3(-2k)+1(2k)}{3+1}, \dfrac{3(4k^2+8)+1(8k^2+16)}{3+1} \right) \\
= & \left(-k, \dfrac{20k^2+40}{4} \right) \\
= & (-k, 5k^2+10)
\end{array}$

