2022-I-18

1. 利用餘弦公式，可得

   $\begin{array}{rcl}
   QR^2 & = & PR^2 +PQ^2 -2(PR)(PQ)\cos \angle QPR \\
   QR^2 & = & 25^2 +30^2 -2(25)(30)\cos 95^\circ \\
   QR & = & 40.690\ 706\ 73\text{ cm}
   \end{array}$

2. 利用正弦公式，可得

   $\begin{array}{rcl}
   \dfrac{PR}{\sin \angle PQR} & = & \dfrac{QR}{\sin \angle QPR} \\
   \dfrac{25}{\sin \angle PQR} & = & \dfrac{40.690\ 706\ 73}{\sin 95^\circ} \\
   \angle PQR & = & 37.738\ 093\ 75^\circ
   \end{array}$

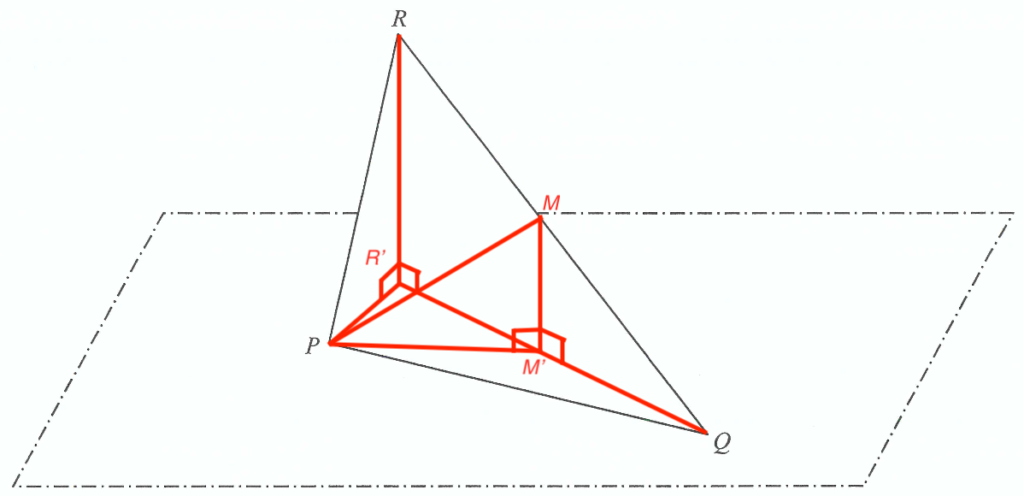
留意所求的角為 $\angle MPM’$。

在 $\Delta MPQ$ 中，

$\begin{array}{rcl}
MP^2 & = & PQ^2 +QM^2 -2(PQ)(QM)\cos \angle PQM \\
MP^2 & = & 30^2 +\left(\dfrac{40.690\ 706\ 73}{2}\right)^2 -2(30)\left(\dfrac{40.690\ 706\ 73}{2}\right) \cos 37.738\ 093\ 75^\circ \\
MP & = & 18.669\ 938\ 31\text{ cm}
\end{array}$

由於 $RR’\text{//}MM’$ 及 $M$ 為 $QR$ 的中點，可得

$\begin{array}{rcl}
MM’ & = & \dfrac{1}{2} RR’ \\
MM’ & = & \dfrac{1}{2} PR \sin \angle RPR’ \\
MM’ & = & \dfrac{1}{2} (25) \sin 70^\circ \\
MM’ & = & 11.746\ 157\ 76\text{ cm}
\end{array}$

在 $\Delta MPM’$，

$\begin{array}{rcl}
\sin \angle MPM’ & = & \dfrac{MM’}{MP} \\
\sin \angle MPM’ & = & \dfrac{11.746\ 157\ 76}{18.669\ 938\ 31} \\
\angle MPM’ & = & 38.987\ 304\ 93^\circ \\
\angle MPM’ & < & 40^\circ \end{array}$

所以，該宣稱不正確。