2022-I-19

$\begin{array}{rcl}
\dfrac{y-112}{x-83} & = & \dfrac{12-112}{158-83} \\
3y-336 & = & -4x+332 \\
4x+3y -668 & = & 0
\end{array}$

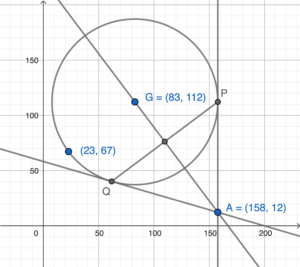
不失其一般性，設 $P$ 為 $A$ 正上方的交點。

$C$ 的半徑

$\begin{array}{cl}
= & \sqrt{(83-23)^2 +(112-67)^2} \\
= & 75
\end{array}$

留意 $AP$ 為鉛垂線，則 $GP$ 為水平線。所以，$P$ 的坐標為 $(158,112)$。

由於 $AG\perp PQ$，可得

$\begin{array}{rcl}
m_{PQ} \times m_{AG} & = & -1 \\
m_{PQ} \times \dfrac{-4}{3} & = & -1 \\
m_{PQ} & = & \dfrac{3}{4}
\end{array}$

所以，通過 $P$ 及 $Q$ 的直線的方程為

$\begin{array}{rcl}
\dfrac{y-112}{x-158} & = & \dfrac{3}{4} \\
4y-448 & = & 3x-474 \\
3x-4y-26 & = & 0
\end{array}$

對於 $AG$ 與 $PQ$ 的交點，

$\left\{ \begin{array}{ll}
4x+3y-668=0 & \ldots \unicode{x2460} \\
3x-4y-26=0 & \ldots \unicode{x2461}
\end{array}\right.$

$4\times \unicode{x2460} +3 \times \unicode{x2461}$，可得

$\begin{array}{rcl}
25x -2750 & = & 0 \\
x & = & 110
\end{array}$

把 $x=110$ 代入 $\unicode{x2460}$，可得

$\begin{array}{rcl}
4(110)+3y-668 & = & 0 \\
y & = & 76
\end{array}$

所以，該交點的坐標為 $(110, 76)$。

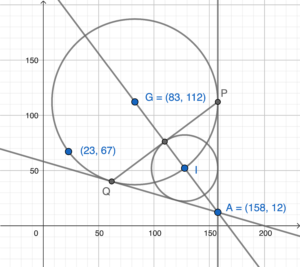
留意 $I$ 的 $x$ 坐標為 $158-r$。也留意 $I$ 在 $AG$ 之上。把 $x=158-r$ 代入 $4x+3y-668=0$，可得

$\begin{array}{rcl}
4(158-r)+3y-668 & = & 0 \\
632-4r+3y-668 & = & 0 \\
3y & = & 4r+36 \\
y & = & \dfrac{4r+36}{3}
\end{array}$

所以，$I=\left(158-r, \dfrac{4r+36}{3}\right)$。

考慮 $\Delta APQ$ 的內切圓的半徑，可得

$\begin{array}{rcl}
((158-r)-110)^2 +\left(\dfrac{4r+36}{3} -76\right)^2 & = & r^2 \\
(48-r)^2 + \left( \dfrac{4r-192}{3}\right)^2 & = & r^2 \\
20736 -864r +9r^2 +16r^2-1536r+36864 -r^2 & = & 0 \\
16r^2-2400r +57600 & = & 0 \\
r^2 -150r +3600 & = & 0 \\
(r-30)(r-120) & = & 0
\end{array}$

$\therefore r=30$ 或 $r=120$ (捨去)。

所以，$I=(128,52)$。

由此，該內切圓的方程為 $(x-128)^2+(y-52)^2=900$。

由於，通過 $A$、$P$、$G$ 及 $Q$ 的圓為 $\Delta APQ$ 的外接圓。

由於 $\angle APG =90^\circ$，則 $AG$ 為外接圓的直徑。

由於所有圓形均相似，可得

$\begin{array}{cl}
& \text{內切圓的面積} : \text{外接圓的面積} \\
= & (\text{內切圓的半徑})^2 : (\text{外接圓的半徑})^2 \\
= & 30^2 : \left(\dfrac{AG}{2}\right)^2 \\
= & 900 : \dfrac{1}{4}[(83-158)^2+(112-12)^2] \\
= & 900 : 3906.25 \\
= & 144 : 624 \\
\neq & 1:4
\end{array}$

所以，不同意該宣稱，