答案:B
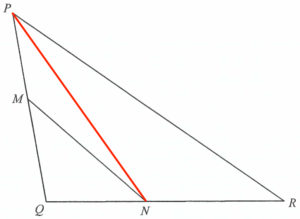
連結 $PN$。

設 $x\text{ cm}^2$ 為 $\Delta MNQ$ 的面積。由於 $\Delta MNP$ 及 $\Delta MNQ$ 若分別以 $MP$ 及 $MQ$ 為底的話,它們會有相同的高,所以
$\begin{array}{rcl}
\dfrac{\text{$\Delta MNP$ 的面積}}{\text{$\Delta MNQ$ 的面積}} & = &\dfrac{PM}{MQ} \\
\dfrac{\text{$\Delta MNP$ 的面積}}{x} & =& \dfrac{5}{6} \\
\text{$\Delta MNP$ 的面積} & = & \dfrac{5x}{6} \text{ cm}^2
\end{array}$
由於 $\Delta NPR$ 及 $\Delta NPQ$ 若分別以 $NR$ 及 $NQ$ 為底的話,它們會有相同的高,所以
$\begin{array}{rcl}
\dfrac{\text{$\Delta PNR$ 的面積}}{\text{$\Delta NPQ$ 的面積}} & = &\dfrac{NR}{NQ} \\
\dfrac{59 -\frac{5x}{6}}{x+\frac{5x}{6}} & =& \dfrac{4}{3} \\
177-\dfrac{5x}{2} & = & 4x +\dfrac{10x}{3} \\
\dfrac{59}{6} x & = & 177 \\
x & = & 18
\end{array}$
所以,$\Delta MNQ$ 的面積為 $18\text{ cm}^2$。

