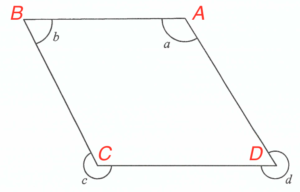
如圖所示,把四個頂點記為 $A$、$B$、$C$ 及 $D$。
I 必為正確。由於 $AD\text{//} BC$,則 $a+b=180^\circ \text{ (同旁內角,$AD$//$BC$)}$。
II 不一定正確。假定 $b=30^\circ$。可得
$\begin{array}{rcll}
\angle BCD +b & = & 180^\circ & \text{(同旁內角,$AB$//$DC$)} \\
\angle BCD & = & 180^\circ -b \\
\angle BCD & = & 180^\circ -30\circ \\
\angle BCD & = & 150^\circ
\end{array}$
另外,
$\begin{array}{rcll}
\angle BCD +c & = & 360^\circ & \text{(同頂角)} \\
150^\circ +c & = & 360^\circ \\
c & = & 210^\circ
\end{array}$
所以在這情況,$b+c \neq 360^\circ$。
III 必為正確。留意 $\angle ADC = b \text{ (平行四邊形的對角)}$。
$\begin{array}{rcll}
\text{relfex} \angle BCD +\angle BCD + \text{reflex} \angle ADC +\angle ADC & = & 720^\circ \\
c +180^\circ -b +d +b & = & 720^\circ \\
b+c & = & 540^\circ
\end{array}$

