2022-M2-12

$\begin{array}{cl}
& \av{AD} \\
= & \dfrac{b\av{AB}+c\av{AC}}{b+c} \\
= & \dfrac{b}{b+c}(\av{OB}-\av{OA})+\dfrac{c}{b+c}(\av{OC}-\av{OA}) \\
= & \dfrac{-(b+c)}{b+c}\av{OA}+\dfrac{b}{b+c}\av{OB}+\dfrac{c}{b+c}\av{OC} \\
= & -\av{OA}+\dfrac{b}{b+c}\av{OB}+\dfrac{c}{b+c}\av{OC}
\end{array}$

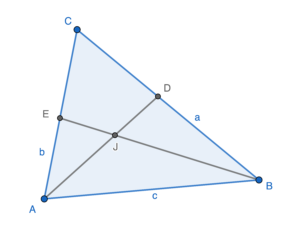
$\begin{array}{cl}
& \av{AJ} \\
= & \av{OJ}-\av{OA} \\
= & \dfrac{a}{a+b+c}\av{OA}+\dfrac{b}{a+b+c}\av{OB}+\dfrac{c}{a+b+c}\av{OC}-\av{OA} \\
= & \dfrac{-(b+c)}{a+b+c}\av{OA}+\dfrac{b}{a+b+c}\av{OB}+\dfrac{c}{a+b+c}\av{OC} \\
= & \dfrac{b+c}{a+b+c}\left(-\av{OA}+\dfrac{b}{b+c}\av{OB}+\dfrac{c}{b+c}\av{OC} \right) \\
= & \dfrac{b+c}{a+b+c}\av{AD}
\end{array}$

由於 $a$、$b$ 及 $c$ 為正實數，則 $0 < \dfrac{b+c}{a+b+c} < 1$。

由此，$\av{AJ}=t\av{AD}$，其中 $t\in(0,1)$。

所以，$J$ 在 $AD$ 之上。

透過比較 (a) 與 (a)(ii) 的條件，可得 $AE:EC=c:a$。則利用 (a)(i) 中相同的做法，可得

$\begin{array}{rcl}
\av{BE} & = & \dfrac{a}{a+c}\av{OA}-\av{OB}+\dfrac{c}{a+c}\av{OC}
\end{array}$

所以，可得

$\begin{array}{cl}
& \av{BJ} \\
= & \av{OJ}-\av{OB} \\
= & \dfrac{a}{a+b+c}\av{OA}+\dfrac{b}{a+b+c}\av{OB}+\dfrac{c}{a+b+c}\av{OC}-\av{OB} \\
= & \dfrac{a}{a+b+c}\av{OA}+\dfrac{-(a+c)}{a+b+c}\av{OB}+\dfrac{c}{a+b+c}\av{OC} \\
= & \dfrac{a+c}{a+b+c}\left(\dfrac{a}{a+c}\av{OA}-\av{OB}+\dfrac{c}{a+c}\av{OC}\right) \\
= & \dfrac{a+c}{a+b+c}\av{BE}
\end{array}$

由於 $a$、$b$ 及 $c$ 為正實數，則 $0 < \dfrac{a+c}{a+b+c} < 1$。

由此，$\av{BJ}=t\av{BE}$，其中 $t\in(0,1)$。

所以，$J$ 在 $BE$ 之上。

由此，$AD$ 與 $BE$ 相交於 $J$。

在 (b) 中，$I$ 為 $\Delta ABC$ 的內心。由此，可得

$\begin{array}{rcl}
\av{OI} & = & \dfrac{a}{a+b+c}\av{OA}+\dfrac{b}{a+b+c}\av{OB}+\dfrac{c}{a+b+c}\av{OC} \ \ldots \unicode{x2460}
\end{array}$

$\begin{array}{cl}
& a \\
= & BC \\
= & |\av{OC}-\av{OB}| \\
= & | -3\bv{j}+\bv{k}-40\bv{i}+3\bv{j}-\bv{k}| \\
= & |-40\bv{i}| \\
= & 40
\end{array}$

$\begin{array}{cl}
& b \\
= & AC \\
= & |\av{OC}-\av{OA}| \\
= & |-3\bv{j}+\bv{k}-35\bv{i}-9\bv{j}-\bv{k}| \\
= & |-35\bv{i}-12\bv{j}| \\
= & \sqrt{(-35)^2+(-12)^2} \\
= & 37
\end{array}$

$\begin{array}{cl}
& c \\
= & AB \\
= & |\av{OB}-\av{OA}| \\
= & |40\bv{i}-3\bv{j}+\bv{k}-35\bv{i}-9\bv{j}-\bv{k}| \\
= & |5\bv{i}-12\bv{j}| \\
= & \sqrt{(5)^2+(-12)^2} \\
= & 13
\end{array}$

由此，從 $\unicode{x2460}$，可得

$\begin{array}{cl}
& \av{OI} \\
= & \dfrac{40}{40+37+13}(35\bv{i}+9\bv{j}+\bv{k})+\dfrac{37}{40+37+13}(40\bv{i}-3\bv{j}+\bv{k})+\dfrac{13}{40+37+13}(-3\bv{j}+\bv{k}) \\
= & 32\bv{i}+\dfrac{7}{3}\bv{j}+\bv{k}
\end{array}$

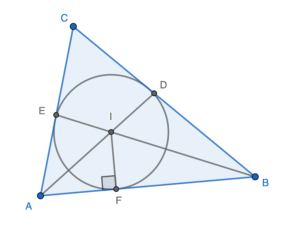
考慮 $\Delta AFI$，

$\begin{array}{cl}
\sin \angle FAI & = & \dfrac{FI}{AI} \\
FI & = & AI\sin \angle FAI \ \ldots \unicode{x2461}
\end{array}$

另外，

$\begin{array}{cl}
& \av{AI}\times \av{AB} \\
= & (\av{OI}-\av{OA})\times \av{AB} \\
= & \left(32\bv{i}+\dfrac{7}{3}\bv{j}+\bv{k}-35\bv{i}-9\bv{j}-\bv{k}\right)\times (5\bv{i}-12\bv{j}) \\
= & \left(-32\bv{i}-\dfrac{20}{3}\bv{j}\right)\times (5\bv{i}-12\bv{j}) \\
= & \begin{vmatrix} \bv{i} & \bv{j} & \bv{k} \\ -3 & \dfrac{-20}{3} & 0 \\ 5 & -12 & 0 \end{vmatrix} \\
= & \bv{k} \begin{vmatrix} -3 & \dfrac{-20}{3} \\ 5 & -12 \end{vmatrix} \\
= & \dfrac{208}{3}\bv{k}
\end{array}$

與此同時，

$\begin{array}{rcl}
|\av{AI}\times \av{AB}| & = & (AI)(AB)\sin\angle BAI \\
\left|\dfrac{208}{3}\bv{k}\right| & = & 13(AI)\sin\angle FAI \\
AI\sin \angle FAI & = & \dfrac{16}{3} \ \ldots \unicode{x2462}
\end{array}$

利用 $\unicode{x2461}$ 及 $\unicode{x2462}$，可得 $FI=\dfrac{16}{3}$。

所以，該內接圓的半徑為 $\dfrac{16}{3}$。