2023-I-12

$\begin{array}{rcl}
f(10) & = & 62 \\
k_1+k_2(10)^2 & = & 62 \\
k_1 +100k_2 & = & 62 \ldots \unicode{x2460}
\end{array}$

另外，

$\begin{array}{rcl}
f(15) & = & 122 \\
k_1 +k_2(15)^2 & = & 122 \\
k_1 +225k_2 & = & 122 \ldots \unicode{x2461}
\end{array}$

$\unicode{x2461} -\unicode{x2460}$，可得

$\begin{array}{rcl}
125k_2 & = & 60 \\
k_2 & = & \dfrac{12}{25}
\end{array}$

把 $k_2=\dfrac{12}{25}$ 代入 $\unicode{x2460}$，可得

$\begin{array}{rcl}
k_1 +100\left(\dfrac{12}{25} \right) & = & 62 \\
k_1 & = & 14
\end{array}$

所以，$f(x) =14+\dfrac{12}{25}x^2$。

由此，可得

$\begin{array}{rcl}
f(5) & = & 14 +\dfrac{12}{25} \times (5)^2 \\
f(5) & = & 26
\end{array}$

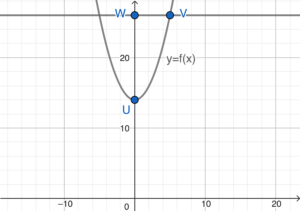
留意 $U$ 為 $y=f(x)$ 的圖像的 $y$ 截距，所以 $U$ 的坐標為 $(0,14)$。

利用 (a) 的結果，$V$ 的坐標為 $(5,26)$。

由於 $\angle UWV=90^\circ$，所以 $UV$ 為 $C$ 的一直徑。

$C$ 的半徑

$\begin{array}{cl}
= & \dfrac{1}{2} UV \\
= & \dfrac{1}{2} \sqrt{(5-0)^2+(26-14)^2} \\
= & \dfrac{13}{2}
\end{array}$

由此，$C$ 的圓周

$\begin{array}{cl}
= & 2\pi \times \dfrac{13}{2} \\
= & 13\pi
\end{array}$