2023-I-14

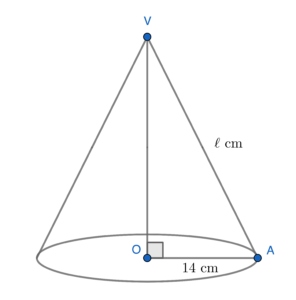
設 $\ell \text{ cm}$ 為圓錐體的斜高。可得

$\begin{array}{rcl}
\pi (14)(\ell) & = & 700\pi \\
\ell & = & 50
\end{array}$

所以，圓錐體的斜高為 $50\text{ cm}$。

圓錐體的高

$\begin{array}{cl}
= & \sqrt{50^2 -14^2} \\
= & 48\text{ cm}
\end{array}$

1. 依題意略繪下圖。
   

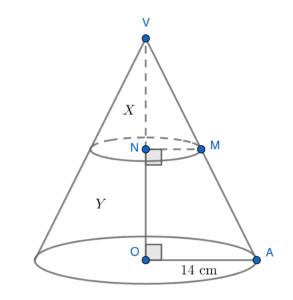
   原來的圓錐體的體積

   $\begin{array}{cl}
   = & \dfrac{1}{3} \pi(14)^2(48) \\
   = & 3136\pi \text{ cm}^3
   \end{array}$

   $X$ 的曲面面積

   $\begin{array}{cl}
   = & 700\pi \times \dfrac{1}{1+15} \\
   = & \dfrac{175}{4}\pi\text{ cm}^2
   \end{array}$

   由於 $X$ 與一竹日木來的圓錐體相似，可得

   $\begin{array}{rcl}
   \left(\dfrac{\text{原來的圓錐體的體積}}{\text{$X$ 的體積}}\right)^2 & = & \left(\dfrac{\text{原來的圓錐體的曲面面積}}{\text{$X$ 的曲面面積}}\right)^3 \\
   \left( \dfrac{3136\pi}{\text{$X$ 的體積}}\right)^2 & = & \left( \dfrac{700\pi}{\frac{175}{4}\pi}\right)^3 \\
   \text{volume of $X$} & = & 49\pi \text{ cm}^3
   \end{array}$

   由此，$Y$ 的體竹木一手金

   $\begin{array}{cl}
   = & 3136\pi -49\pi \\
   = & 3087\pi\text{ cm}^3
   \end{array}$

2. 設 $r\text{ cm}$ 為兩個球體的半徑。

   $\begin{array}{rcl}
   2 \times \dfrac{4}{3} \pi r^3 & = & 3087\pi \\
   r^3 & = & \dfrac{9261}{8} \\
   r & = & \dfrac{21}{2}
   \end{array}$

   由此，該兩個球體的直徑

   $\begin{array}{cl}
   = & 2 \times \dfrac{21}{2} \\
   = & 21\text{ cm}
   \end{array}$