2023-I-17

$\begin{array}{rcl}
\dfrac{WX}{\sin \angle WYX} & = & \dfrac{XY}{\sin \angle XWY} \\
\dfrac{6}{\sin 70^\circ} & = & \dfrac{5}{\sin \angle XWY} \\
\sin \angle XWY & = & \dfrac{5\sin 70^\circ}{6} \\
\angle XWY & = & 51.543\ 189\ 37^\circ
\end{array}$

已 知 $WZ$ 與 $\Delta WXY$ 的交角為 $30^\circ$。則 $\angle ZWZ’ =30^\circ$。在 $\Delta WZZ’$ 中，可得

$\begin{array}{rcl}
\tan \angle ZWZ’ & = & \dfrac{ZZ’}{WZ’} \\
ZZ’ & = & WZ’ \tan 30^\circ \ldots \unicode{x2460}
\end{array}$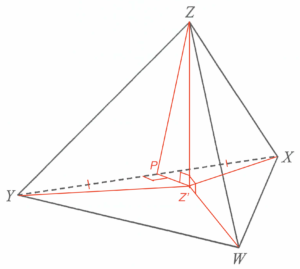

設 $P$ 為 $XY$ 的中點。

由於 $WZ=XZ=YZ$，則 $WZ’=XZ’=YZ’$。所以 $Z’$ 為 $\Delta WXY$ 的外心。

由此，$PZ’$ 為 $XY$ 的垂直平分線。

所以，$\Delta WXY$ 與 $\Delta XYZ$ 的交角為 $\angle ZPZ’$。

由於 $Z’$ 為 $\Delta WXY$ 的外心，所以 $\angle XZ’Y = 2 \angle XWY$ (圓心角兩倍於圓周角)。

留意 $\Delta PXZ’ \cong \Delta PYZ’$，所以 $\angle PZ’X = \angle PZ’Y$ ($\cong\Delta$ 的對應角)。

由此，$\angle PZ’Y = \angle XWY$。

在 $\Delta PYZ’$ 中，

$\begin{array}{rcl}
\cos \angle PZ’Y & = & \dfrac{PZ’}{YZ’} \\
PZ’ & = & YZ’ \cos \angle PZ’Y \\
PZ’ & = & WZ’ \cos \angle XWY \ldots \unicode{x2461}
\end{array}$

在 $\Delta PZZ’$ 中，

$\begin{array}{rcll}
\tan \angle ZPZ’ & = & \dfrac{ZZ’}{PZ’} \\
\tan \angle ZPZ’ & = & \dfrac{WZ’ \tan 30^\circ}{ WZ’ \cos \angle XWY} & \text{，把 $\unicode{x2460}$ 及 $\unicode{x2461}$ 代入} \\
\tan \angle ZPZ’ & = & \dfrac{\tan 30^\circ}{\cos 51.543\ 189\ 37^\circ} \\
\angle ZPZ’ & = & 42.871\ 428\ 55^\circ \\
\angle ZPZ’ & < &45^\circ \end{array}$

$\therefore \Delta WXY$ 與 $XYZ$ 的交角不超過 $45^\circ$。