- 由於 $OQ$ 為 $\Delta OPR$ 的中線,則 $Q$ 為 $PR$ 的中點。設 $R=(a,b)$。利用中點公式,可得
$\begin{array}{rcl}
32 & = & \dfrac{a+50}{2} \\
64 & = & a +50 \\
a & = & 14
\end{array}$另外,
$\begin{array}{rcl}
t & = & \dfrac{b+0}{2} \\
b & = & 2t
\end{array}$所以,$R=(14,2t)$。
由於 $OP$ 為一水平線,則 $RH$ 為一鉛垂線。由此,$H$ 的 $x$ 坐標
$\begin{array}{cl}
= & $R$ \text{ 的 }x\text{坐標} \\
= & 14
\end{array}$設 $H=(14,d)$。由於 $OH \perp PR$,可得
$\begin{array}{rcl}
m_{OH} \times m_{PR} & = & -1 \\
\dfrac{d-0}{14-0}\times \dfrac{2t-0}{14-50} & = & -1 \\
dt & = & 252 \\
d & = & \dfrac{252}{t}
\end{array}$所以,$H$ 的坐標為 $\left(15, \dfrac{252}{t}\right)$。
由於 $OP$ 為一水平線,則 $OP$ 的垂直平分線為一鉛垂線。由此,$G$ 的 $x$ 坐標
$\begin{array}{cl}
= & \dfrac{0+50}{2} \\
= & 25
\end{array}$設 $G=(25,c)$。由於 $Q$ 為 $PR$ 的中點,則 $GQ$ 為 $PR$ 的垂直平分線。由此,可得
$\begin{array}{rcl}
m_{GQ} \times m_{PR} & = & -1 \\
\dfrac{c-t}{25-32} \times \dfrac{2t-0}{14-50} & = & -1 \\
t(c-t) & = & -126 \\
c & = & t-\dfrac{126}{t} \\
c & = & \dfrac{t^2-126}{t}
\end{array}$所以,$G$ 的坐標為 $\left(25, \dfrac{t^2-126}{t} \right)$。
- 依題意略繪下圖。
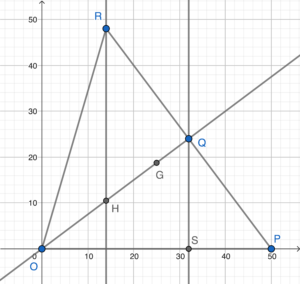
- 由於 $\angle PQS = \angle POQ$,可得
$\begin{array}{rcl}
\tan \angle PQS & = & \tan \angle POQ \\
\dfrac{PS}{QS} & = & \dfrac{QS}{SO} \\
\dfrac{50-32}{t-0} & = & \dfrac{t-0}{32-0} \\
t^2 & = & 576
\end{array}$$\therefore t=24$ 或 $t=-24$ (捨去)。
- 留意 $G$ 及 $Q$ 的坐標分別為 $\left(25, \dfrac{75}{4}\right)$ 及 $(32,24)$。
$OG$ 的斜率
$\begin{array}{cl}
= & \dfrac{\frac{75}{4}-0}{25-0} \\
= & \dfrac{3}{4}
\end{array}$$OQ$ 的斜率
$\begin{array}{cl}
= & \dfrac{24-0}{32-0} \\
= & \dfrac{3}{4}
\end{array}$由於 $m_{OG} =m_{OQ}$ 及 $O$ 為公共點,所以 $O$、$G$ 及 $Q$ 共線。
- 在圖中加入 $\angle OPR$ 的角平分線。設 $J$ 為 $I$ 在 $OP$ 的垂足。
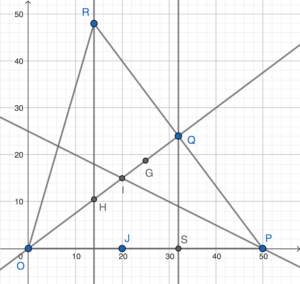
由於 $OQ\perp PQ$ 及 $IJ \perp OP$,所以 $QP$ 及 $JP$ 分別為 $\Delta OPR$ 內切圓於 $Q$ 及 $J$ 的切線。
$\begin{array}{rcl}
QP & = & \sqrt{(32-50)^2+(24-0)^2} \\
QP & = & 30
\end{array}$所以,$J$ 的坐標為 $(50-30, 0)$,即 $(20,0)$。
由於 $IJ$ 為鉛垂線,則 $I$ 及 $J$ 的 $x$ 坐標相等。設 $I=(20,e)$。
留意 $IJ$ 及 $IQ$ 為 $\Delta OPR$ 內切圓的半徑。
$\begin{array}{rcl}
IJ & = & IQ \\
e & = & \sqrt{(32-20)^2+(24-e)^2} \\
e^2 & = & 144 +576-48e+e^2 \\
48e & = & 720 \\
e & = & 15
\end{array}$所以,$I$ 的坐標為 $(20,15)$。
利用 (a) 及 (b)(i) 的結果,$H$ 的坐標 $\left(14,\dfrac{21}{2}\right)$。
由於 $OQ$ 為 $PR$ 的垂直平分線,可得 $PQ=RQ$ 及 $OQ\perp PR$。
$\begin{array}{cl}
& \text{$\Delta GHR$ 的面積} : \text{$\Delta IPQ$ 的面積} \\
= & \dfrac{1}{2}(GH)(RQ) : \dfrac{1}{2} (IQ)(PQ) \\
= & GH : IQ \\
= & \sqrt{(25-14)^2+\left(\dfrac{75}{4}-\dfrac{21}{2}\right)^2} : \sqrt{(32-20)^2+(24-15)^2} \\
= & \dfrac{55}{4} : 15 \\
= & 11 : 12
\end{array}$
- 由於 $\angle PQS = \angle POQ$,可得
2023-I-19
答案:(a) $G=\left(25,\dfrac{t^2-126}{t}\right)$, $H=\left(14, \dfrac{252}{t}\right)$ (b) (ii) 是 (iii) $11:12$

