將大圓的圓心記為 $O$。
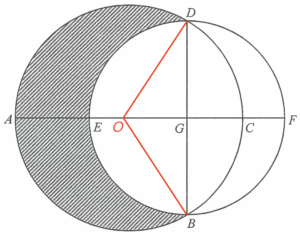
由於 $AC$ 為大圓的一直徑,可得
$\begin{array}{rcl}
2AO & = & AC \\
2AO & = & AG+CG \\
2AO & = & 30+10\\
AO & = & 20\text{ cm}
\end{array}$
留意 $OA$ 及 $OC$ 大圓的半徑,可得
$\begin{array}{rcl}
OC & = & OA \\
OG +CG & = & OA \\
OG +10 & = & 20 \\
OG & = & 10\text{ cm}
\end{array}$
由於 $EF$ 及 $BD$ 均為小圓的直徑,則 $G$ 為小圓的圓心。由此,$DG$ 及 $BG$ 為小圓的半徑。
由於 $G$ 為 $BD$ 的中點,且 $O$ 為大圓的圓心,所以 $\angle OGD= 90^\circ$ $\text{(圓心至弦中點的連線垂直圓)}$.
在 $\Delta ODG$ 中,
$\begin{array}{rcl}
DG^2 & = & OD^2 -OG^2 \\
DG^2 & = & 20^2-10^2 \\
DG & = & \sqrt{300}\text{ cm}
\end{array}$
另外,
$\begin{array}{rcl}
\cos \angle DOG & = & \dfrac{OG}{OD} \\
\cos \angle DOG & = & \dfrac{10}{20} \\
\angle DOG & = & 60^\circ
\end{array}$
留音 $\Delta DGO \cong \Delta BGO$。所以 $\angle BOG=\angle DOG$ 及 $\angle BOD =120^\circ$。
弓形 $BCD$ 的面積
$\begin{array}{cl}
= & \text{$OBCD$ 扇形的面積} -\text{$\Delta OBD$ 的面積} \\
= & \pi (OB)^2 \dfrac{\angle BOD}{360^\circ} -\dfrac{1}{2} (BD) (OG) \\
= & \pi (20)^2 \dfrac{120^\circ}{360^\circ} -\dfrac{1}{2}\times 2\sqrt{300} \times 10 \\
= & 245.673\ 939\ 7\text{ cm}^2
\end{array}$
半圓 $BEDG$ 的面積
$\begin{array}{cl}
= & \dfrac{1}{2}\pi (BG)^2 \\
= & \dfrac{1}{2} \pi (\sqrt{300})^2 \\
= & 471.238\ 898 \text{ cm}^2
\end{array}$
陰影部分的面積
$\begin{array}{cl}
= & \pi (20)^2 -471.238\ 898-245.673\ 939\ 7 \\
= & 539.724\ 223\ 7\text{ cm}^2 \\
\approx & 540\text{ cm}^2
\end{array}$

