連結 $R$ 及 $X$。設 $PX:XQ =r:1$,其中 $r>0$。
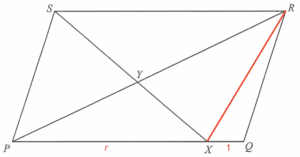
由於 $\Delta PQR$ 及 $\Delta RQX$ 分別以 $PX$ 及 $XQ$ 為底的話,它們有相同的高,可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta PQR$ 的面積}}{\text{$\Delta QRX$ 的面積}} & = & \dfrac{PQ}{XQ} \\
\dfrac{32+58}{\text{$\Delta QRX$ 的面積}} & = & \dfrac{1+r}{1} \\
\text{$\Delta QRX$ 的面積} & = & \dfrac{90}{1+r}
\end{array}$
由於 $\Delta PXY \sim \Delta RSY$,可得
$\begin{array}{rcl}
\dfrac{PY}{RY} & = & \dfrac{PX}{RS} \\
\dfrac{PY}{RY} & = & \dfrac{r}{1+r}
\end{array}$
由於 $\Delta PXY$ 及 $\Delta RXY$ 分別以 $PY$ 及 $RY$ 為底的話,它們有相同的高,可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta PXY$ 的面積}}{\text{$\Delta RXY$ 的面積}} & = & \dfrac{PY}{RY} \\
\dfrac{32}{\text{$\Delta RXY$ 的面積}} & = & \dfrac{r}{1+r} \\
\text{$\Delta RXY$ 的面積} & = & \dfrac{32(1+r)}{r}
\end{array}$
由此,可得
$\begin{array}{rcl}
\text{$\Delta QRX$ 的面積}+\text{$\Delta RXY$ 的面積} & = & \text{$QRYX$ 的面積} \\
\dfrac{90}{1+r}+\dfrac{32(1+r)}{r}& = & 58 \\
90r+32(1+r)^2 & = & 58r(1+r) \\
90r +32+64r+32r^2 -58r-58r^2 & = & 0 \\
-26r^2+96r+32 & = & 0 \\
13r^2-48r-16 & = & 0 \\
(r-4)(13r+4) & = & 0
\end{array}$
$\therefore r=4$ 或 $r=\dfrac{-4}{13}$ (捨去)。
由於 $\Delta PXY \sim \Delta RSY$,可得
$\begin{array}{rcl}
\dfrac{\text{$\Delta PXY$ 的面積}}{\text{$\Delta RSY$ 的面積}} & = & \left(\dfrac{PX}{RS}\right)^2 \\
\dfrac{32}{\text{$\Delta RSY$ 的面積}} & = & \left(\dfrac{4}{1+4}\right)^2 \\
\text{$\Delta RSY$ 的面積} & = & 50 \text{ cm}^2
\end{array}$

